Рассеивают кванты главным образом свободные электроны. Эффективное
сечение рассеяния (Томсоновское сечение рассеяния) можно оценить по
классическому радиусу электрона 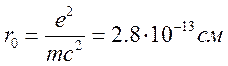 и
и 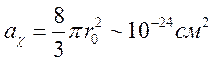 . Ему соответствует
. Ему соответствует ![]() см
–1 (для полностью ионизированной плазмы), и только для
сильноразреженной, полностью ионизированной плазмы
см
–1 (для полностью ионизированной плазмы), и только для
сильноразреженной, полностью ионизированной плазмы ![]() становится
сравнимым с kvтор. Это
имеет место в звездных коронах, в земных условиях рассеянием света
практически всегда можно пренебречь по сравнению с поглощением в газе.
становится
сравнимым с kvтор. Это
имеет место в звездных коронах, в земных условиях рассеянием света
практически всегда можно пренебречь по сравнению с поглощением в газе.
Теперь рассмотрим баланс между поглощением и испусканием света в газе. Количество поглощаемой лучистой энергии есть
![]() (13.3).
(13.3).
Количество энергии самопроизвольно (спонтанно) испускаемой веществом есть
![]() (13.4),
(13.4),
где jvcn определяется
только свойствами вещества и его состоянием. Однако в газах помимо спонтанного
испускания существует вынужденное (или индуцированное) лучеиспускание.
Присутствующие кванты как бы способствуют переходам между возмущенным
электронным состояниям в атомах, сопровождающимися испусканием таких же самых
квантов. Эта ситуация может быть качественно объяснена в рамках волнового
представления излучения: спонтанно излучающие атомы могут быть представлены как
системы осцилляторов, находящихся во внешнем поле электромагнитной волны. В
этом случае возможно резонансное возбуждение осциллятора с последующим излучением
электромагнитной волны того же направления и частоты. В квантовой механике
получено, что полная энергия, испускаемая единицей объема вещества в единицу
времени в телесном угле ![]() есть
есть
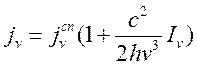 (13.5).
(13.5).
В состоянии термодинамического равновесия, которое выполняется тем точнее, чем выше плотность газа (по крайней мере, когда можно говорить о наличии ЛТР), для равновесного излучения с Ivp должно выполняться балансовое соотношение известное под именем закона Кирхгофа для газов:
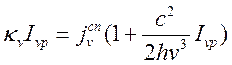 (13.6),
(13.6),
где ![]() определяется свойствами излучающего газа.
Подставляя в (13.6) значение
определяется свойствами излучающего газа.
Подставляя в (13.6) значение ![]() =
= 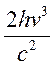
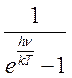 получим
получим
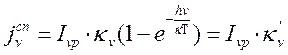 (13.7),
(13.7),
где
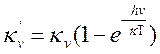 (13.8)
(13.8)
и закон Кирхгофа для газов (13.7) можно переписать в уже привычном виде
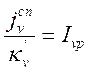 (13.9).
(13.9).
Отсюда видно, что вынужденное испускание можно трактовать как некое
уменьшение поглощения: часть квантов как бы поглощается и тут же испускается
снова с той же частотой и в том же направлении, причем с некоторой
вероятностью, которая согласно (13.8) есть ![]() .
.
Итак, правую часть уравнения переноса (13.2) без членов рассеяния в
приближении ЛТР используя (13.5), (13.7), (13.8) и выражение для ![]() можно переписать:
можно переписать: 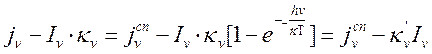 ,
откуда с учетом (13.9) она примет вид
,
откуда с учетом (13.9) она примет вид ![]() , а
само уравнение есть:
, а
само уравнение есть:
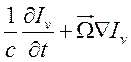 =
= ![]() (13.10).
(13.10).
Получим формальное решение уравнения (13.10), рассматривая Ivp(T) и ![]() (р,Т) как известные функции
координат и времени. Вначале для простоты рассмотрим стационарные уравнения и
найдем решения для излучения вдоль луча в направлении
(р,Т) как известные функции
координат и времени. Вначале для простоты рассмотрим стационарные уравнения и
найдем решения для излучения вдоль луча в направлении ![]() .
.
Вдоль луча s левая часть уравнения (13.10) в стационарном случае
согласно (13.1) есть: 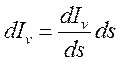 и
и
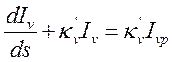 (13.11).
(13.11).
Его решение:
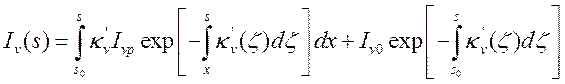 (13.12).
(13.12).
Iv0 – константа интегрирования есть
значение Iv на границе s0 (входящее излучение). Интенсивность
излучения в точке s определяется всеми квантами,
рожденными на длине луча s0 – s и движущиеся в направлении ![]() с
учетом их поглощения на этом пути. От точки х до s
дойдет только доля
с
учетом их поглощения на этом пути. От точки х до s
дойдет только доля 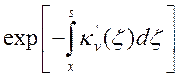 этого излучения, остальное
поглотится на этом пути.
этого излучения, остальное
поглотится на этом пути.
В стационарном случае в точку s к моменту t будут приходить кванты, рожденные в более ранние
моменты времени 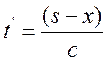 . Из решения (13.12) видно, что
вклад далеких от s источников экспоненциально падает
с возрастанием расстояния, а свет от этих источников проходит за время
. Из решения (13.12) видно, что
вклад далеких от s источников экспоненциально падает
с возрастанием расстояния, а свет от этих источников проходит за время 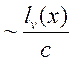 . Это время для наиболее больших lv, связанных с тормозным излучением, составляет
. Это время для наиболее больших lv, связанных с тормозным излучением, составляет
![]() с. и намного меньше характерного времени,
на котором происходит заметное изменение состояния вещества (температуры,
давления и т.д.). Возьмем за характерный газодинамический масштаб тоже
расстояние
с. и намного меньше характерного времени,
на котором происходит заметное изменение состояния вещества (температуры,
давления и т.д.). Возьмем за характерный газодинамический масштаб тоже
расстояние ![]() см, тогда изменение состояния, за счет
газодинамических процессов, произойдет за время
см, тогда изменение состояния, за счет
газодинамических процессов, произойдет за время 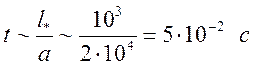 , где а
– скорость звука (
, где а
– скорость звука (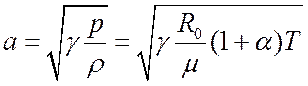 , для воздуха при
, для воздуха при ![]() степень ионизации
степень ионизации ![]() и
и
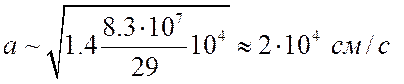 ). Отсюда следует, что при решении задач
РГД можно использовать стационарное уравнение переноса излучения, куда время
входит как параметр, от которого зависят термодинамические свойства вещества,
а, следовательно,
). Отсюда следует, что при решении задач
РГД можно использовать стационарное уравнение переноса излучения, куда время
входит как параметр, от которого зависят термодинамические свойства вещества,
а, следовательно, ![]() и
и ![]() (Т,
р) и уравнение переноса имеет вид
(Т,
р) и уравнение переноса имеет вид
![]() (13.13).
(13.13).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.