Эффекты реактивности, связанные с изменениями технологических параметров реактора, страница 5

                  ω(t) / ω(0) ≈ 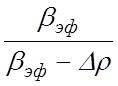 ехр [λt Δρ / (β_эф – Δρ)],                                       (12.1)

если пренебречь переходным процессом, для которого постоянная времени |(Δρ – β_эф) / Λ| » |λ Δρ / (β_эф – Δρ)|. Представив процесс приращения реактивности в виде скачков Δρ через интервалы времени Δ t, изменение мощности реактора во времени приближенно можно записать в виде

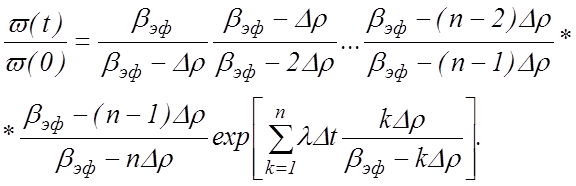                                                  (12.2)

При этом сделано весьма существенное приближение – такая форма записи справедлива, если в реакторе в каждый момент времени существует равновесное состояние между плотностью нейтронов и концентрацией запаздывающих нейтронов. Однако это отношение изменяется слабо. Так, например, для подкритического реактора отношение количества нейтронов в реакторе N к количеству источников запаздывающих нейтронов с составляет N / с = λ Λ / β_эф и не зависит от степени подкритичности реактора. Для надкритичного реактора N / с = λ Λ / (β_эф - ρ). Пологая возмущения реактивности малыми, можно удовлетвориться приведенной зависимостью ω(t), не учитывающей изменения N / с.

Принимая во внимание, что n = t / Δt, и считая Δt « t, получаем

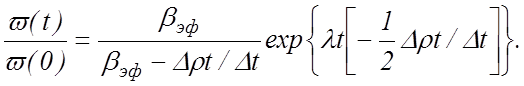                                                          (12.3)

Рассуждая аналогично, можно получить ω(t) / ω(0) и для начальной заданной реактивности ρ₀ > 0 и скорости изменения реактивности + Δρ / Δt:

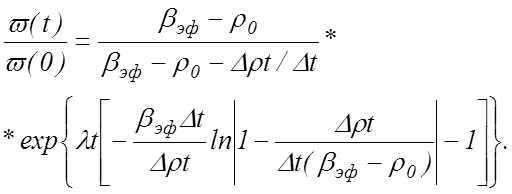                                                   (12.4)

И вообще в указанных выше приближениях, если изменение реактивности задано в виде ρ(t) при ρ(0) ≥0,

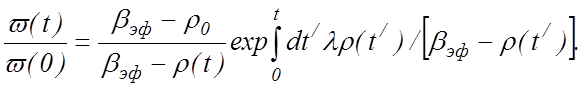                                        (12.5)

При равномерном разогреве реактора с заданной скоростью ΔТ/Δt и температурном коэффициенте реактивности α _t изменение реактивности Δρ / Δt = - α _t ΔТ/Δt. Поскольку ρ₀ « β_эф и индекс представляют такие интервалы времени, при которых | α _t t ΔТ/Δt| ~ | ρ₀ |, то (12.4) можно представить в следующем виде, разложив в ряд логарифмическую функцию:

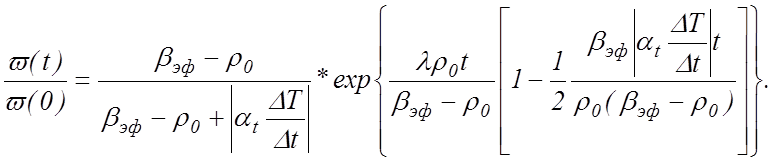                 (12.6)

Мощность имеет максимальное значение при t = t* = ρ₀ / β_эф α _t | ΔТ/Δt |, и в этот момент времени реактивность реактора равна нулю.

Полагая, что ω(t*) / ω(0) ≤ А, и используя (12.6), находим такую реактивность ρ₀, которую надо ввести в реактор, чтобы его мощность не превысила А ω(0):

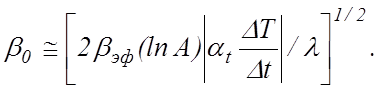                                                                          (12.7)

В частности, если изометрический разогрев ведется со скоростью 5 ⁰С/ч и если диапазон мощностей реактора, в котором возможно изменение, А = 3, то для | α _t | ≈ 5*10 ^–3 β_эф / ⁰С получаем ρ₀ ≈ 1,2 * 10 ^{– 2} β_эф. Время, в течение которого уровень мощности находится в пределах ω(0) ÷ А ω(0), равно 2 t* и для рассматриваемого примера составит ~ 1ч.

Типичный пример измерения ТКР показан на рис. 12.1, где по оси ординат отложена измеренная с помощью цифрового реактиметра реактивность реактора, а по оси абсцисс – измеренная температура. При температуре 245 ⁰С в реактор была введена положительная реактивность ~ 1% β_эф, которая постепенно уменьшалась вследствие роста температуры. Наклон отрезка прямой, проведенной методом наименьших квадратов по измеренным точкам, дает значение ТКР = 0,509% β_эф / ⁰С. Таким методом ТКР может быть измерен с погрешностью ~ 5%, причем основной источник погрешности – неопределенность в показаниях температурных дефектов. Действительно, при изменении температуры на ~ 10 ⁰С реактивность изменится на 5% β_эф. Погрешность измерения реактивности с помощью цифрового реактиметра составляет ± 0,02% β_эф, т.е. относительная погрешность не превышает долей процента, а температуру можно измерить вряд ли лучше, чем с помощью ± 0,5%, что дает вклад в измеряемое значение ТКР ~ 5%.

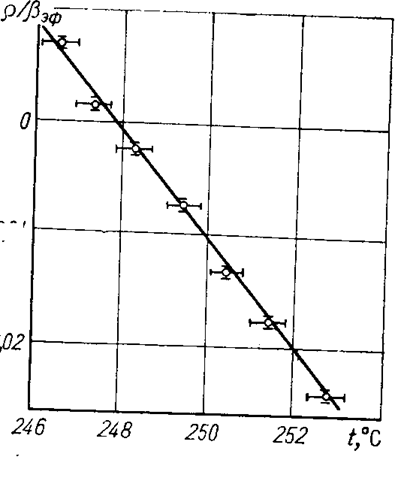
Рис. 12.1. Зависимость реактивности от температуры.