β1=35,49 о и β2=29,16 о
Δβ=180-( β1+ β2)= 180-( 35,49+ 29,16)=115,3 о
Коэффициент потерь энергии в решётки без учёта поправок:
по Δβ=115,3 о и
отношению ![]() =0,703 находим [1] ζ0=0,1.
=0,703 находим [1] ζ0=0,1.
Поправки к ζ0, учитывающие влияние различных параметров на потери [1]:
kM=1.2 – поправка, учитывающая влияние числа Маха на потери;
kα=1 – поправка, учитывающая влияние эффективного угла выхода из рабочей решётки на потери;
kRe=1 – поправка, учитывающая влияние числа Рейнольдса на потери;
Суммарный коэффициент потерь энергии в рабочей решётке для перегретого пара:
ζ пп2= ζ0×kМ×kα×kRe
ζ вп2= ζ2’+ ζ пп2 (2.32)
где:
λ’=0,075 – доля крупнодисперсной влаги в решётке без учёта влияния давления;
kр=0,6 – поправка, учитывающая влияние давления на долю крупнодисперсной влаги;
λ= λ’×kр=0,075×0,6=0,045 – доля крупнодисперсной влаги в решётке с учётом влияния давления;
ζ2’=0,002 – приращение коэффициента потерь от наличия крупнодисперсной влаги.
ζ пп2= 0,1×1,2×1×1
ζ вп2= 0,002+ 0,12=0,122
принимаем ζ 2= ζ вп2.
Коэффициент скорости рабочей решётки:
Ψ=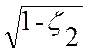 ,
(2.33)
,
(2.33)
Ψ=![]() =0,937.
=0,937.
Действительная скорость выхода потока из рабочей решётки:
W2= Ψ×W2t , (2.34)
W2= 0,937×156,3=146,5 м/с.
Угол направления абсолютной скорости выхода пара из рабочей решётки:
α2=artan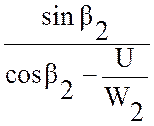 , (2.35)
, (2.35)
где
U=181,898 м/с – окружная скорость ступени.
Α2=artan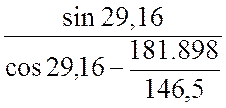 = -52,89 о.
= -52,89 о.
Абсолютная скорость выхода пара из рабочей решётки:
C2=W2×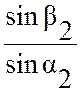 =89.5 м/с.
(2.36)
=89.5 м/с.
(2.36)
Кинетическая энергия пара на выходе из рабочей решётки (ступени):
ΔНвс=С22×(2×10-3), (2.37)
ΔНвс=89,52×(2×10-3)=4 кДж/кг.
Потеря энергии в рабочей решётке:
ΔН2= ζ 2×Нт02, (2.38)
ΔН2= 0,122×12,2=1,491 кДж/кг.
Теплосодержание пара в действительном процессе за рабочей решёткой:
h2=h2t+ΔН2 , (2.39)
h2=2753,5+1,491 кДж/кг.
Параметры пара за рабочей решёткой:
по Р2=3,25 МПа и h2=2755 кДж/кг определяем [4]:
t2=238.2 oC – температура за рабочей решёткой;
ύ2=0,05987 м3/кг – удельный объём за рабочей решёткой;
y2=0.032 – cтепень влажности за рабочей решёткой;
s2=6,0405 кДж/(кг×К) – энтропия за рабочей решёткой.
2.1.6 Расчёт КПД ступени
Располагаемая энергия первой ступени:
Е0=Н0-(sin α2)2×ΔНвс , (2.40)
Е0=50,208-0,636×4=47,662 кДж/кг,
обозначим χ=(sin α2)2=0,636.
Относительный лопаточный КПД:
ηол=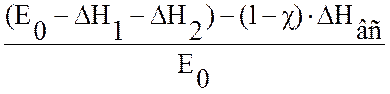 , (2.41)
, (2.41)
ηол=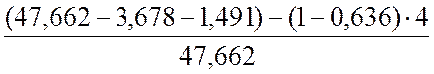 =0,861.
=0,861.
Относительный лопаточный КПД по проекциям скоростей:
ηол’=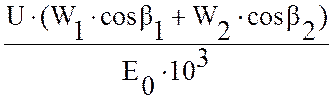 ,
(2.42)
,
(2.42)
ηол’=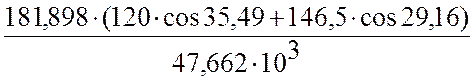 =0,861.
=0,861.
Погрешность теплового расчёта ступени:
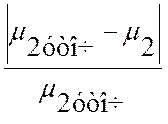 ×100% = 1,289×10-14.
×100% = 1,289×10-14.
2.2 Проверка рабочих лопаток на прочность
Рабочие лопатки паровых турбин работают в очень тяжелых условиях. Как правило, они сильно напряжены и нагреты.
Напряжения в рабочих лопатках возникают как в результате вращения ротора, так и вследствие воздействия аэродинамической нагрузки. В связи с достаточно жесткими условиями эксплуатации, лопатки быстро выходят из строя.
В данном разделе рассматривается расчёт на прочность при воздействии изгибающих нагрузок, в результате которых лопатка меняет свою геометрию ( Рис. 2.2 ).

Рис. 2.2 – Изгиб лопатки (упрощённая модель) .
2.2.1 Допускаемое изгибающее напряжение на рабочих лопатках [8]:
Для сопловых и рабочих лопаток из стали 15Х11МФ:
σ02=670 МПа – предел текучести ( коэффициент запаса ks=1,65 );
σв=815 МПа – предел прочности ( коэффициент запаса kв=3 ).
За минимальное допускаемое изгибающее напряжение в рабочих лопатках принимаем минимальное соотношение:
σн.доп= σв/ kв=271,7 МПа.
Окружное усилие, действующее на рабочие лопатки:
Ru=D’×(W1×cos β1+ W2×cos β2), (2.43)
Ru=365,565×(120×cos 35,49+ 146,5×cos 29,16)=82470,642 Н.
Изгибающее напряжение на лопатках:
σн=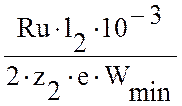 ,
(2.44)
,
(2.44)
σн=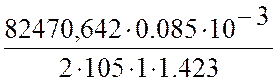 =23,457 МПа.
=23,457 МПа.
Вывод: изгибающее напряжение меньше минимально допустимого (σн< σн.доп), следовательно лопатка пригодна для эксплуатации в данных условиях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.