Расчет площади поверхности охлаждения конденсатора из условий минимальных габаритов (Исследовательская часть дипломного проекта), страница 3

3.1.3.6 Площадь поверхности охлаждения конденсатора:

F=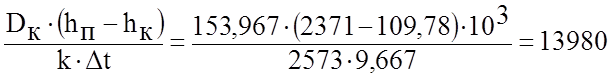м².                   (3.31)

3.1.3.7Определим число трубок в конденсаторе:

N=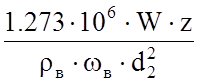,                                                                                 (3.32)

где ρ_в=1000 кг/м³ – плотность охлаждающей воды.

N=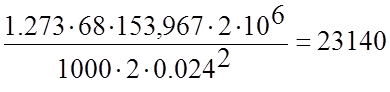шт.

3.1.3.8 Активная длина трубок:

L=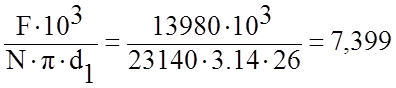м.                                                   (3.33)

3.1.3.9 Удельная паровая нагрузка на конденсатор:

g_п=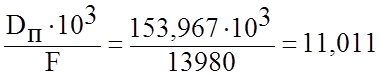г/(м²∙с).                                           (3.34)

Полученная по расчету удельная паровая нагрузка конденсатора близко совпадает с первоначально заданной, и поэтому можно считать расчет законченным и не требующим повторения.

3.1.4 Исходя из выше изложенного внесем следующие изменения в исходные данные расчета по определению площади охлаждения конденсатора и произведем третий расчет:

m = 70 – кратность циркуляции;

d₁ = 22 мм – наружный диаметр трубок;

d₂ = 20 мм – внутренний диаметр трубок;

g_п = 13,914 г/(м² с) – предварительно заданная удельная паровая нагрузка;

3.1.4.1 Из уравнения теплового баланса конденсатора определим нагрев охлаждающей воды:

D_к∙(h_п-h_к)=W∙∆t∙C_p,                                                                                    (3.35)

W=m×D_k,                                                                                                     (3.36)

где h_к=109,78 кДж/кг – энтальпия сконденсировавшегося пара;

      ∆t – нагрев охлаждающей воды, ^oC;

      m = 70 – кратность циркуляции;

      C_p- теплоёмкость воды, равная 4.19 кДж/(кг∙К).

∆t=D_k×(h_п-h_к)/m×D_k×C_p=153,967×(2371-109,78)/70×153,967×4,19=7,710^оС. (3.37)

3.1.4.2 Температура циркуляционной воды на выходе из конденсатора:

t₂=t₁+∆t=12+7,710=19,710 ^оС.                                                                  (3.37)

3.1.4.3 Среднелогарифмическая разность температур:

∆t_л=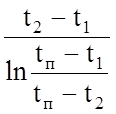,                                                                                           (3.38)

где t_п – температура отработавшего в турбине пара, t_п=26,182 ^оС.

∆t_л=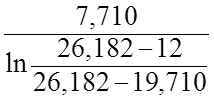 =9,828 ^оС.

3.1.4.4 Коэффициент теплопередачи определяется по формуле Бермана:

k=4070∙a∙Ф_ω∙Ф_t∙Ф_z∙Ф_δ,                                                                              (3.39)

где a – коэффициент чистоты;

      Ф_ω,Ф_t,Ф_z,Ф_δ – множители, учитывающие влияние скорости охлаждающей воды ω_в, ее температуры на входе в конденсатор t₁, числа ходов воды z и удельной паровой нагрузки конденсатора g_п.

а=а_с∙а_м,                                                                                                       (3.40)

где а_с и а_м – коэффициенты, зависящие от ожидаемого состояния поверхности охлаждения и от материала и толщины стенок трубок: а_с=0.8 – при оборотном водоснабжении; а_м=1 – для трубок из латуни и толщиной стенок δ=1 мм.

а=0.8∙1=0.8 .

Ф_ω=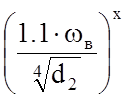,                                                                                          (3.41)

где ω_в=2 м/с – скорость охлаждающей воды, принимается в зависимости от материала трубок;

х=0.12∙а∙(1+0.15∙t₁)= 0.12∙0.8∙(1+0.15∙12)=0,2688.                                 (3.42)

Ф_ω=.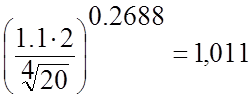

При t₁<35 ^oC                Ф_t=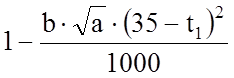 ,                                     (3.43)

где b=0.52-0.0072∙g_п, g_п – удельная паровая нагрузка, г/(м²∙с).           (3.44)

Задаемся предварительно g_п=13,914 г/(м²∙с), находим:

b=0,52-0,0072∙13,914=0,42.

Ф_t=.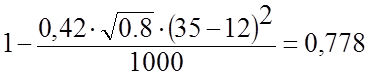

Ф_z=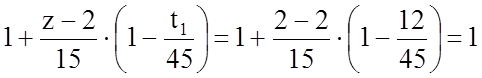.                                       (3.45)

Множитель Ф_δ=1, так как расчет ведется для номинальной нагрузки.

3.1.4.5 Определяем коэффициент теплопередачи k:

k=4070∙0,8∙1,011∙0,778∙1∙1=3200 Вт/(м²∙К).                                            (3.46)

3.1.4.6 Площадь поверхности охлаждения конденсатора:

F=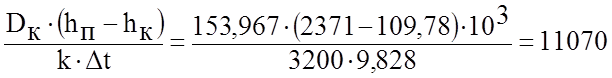м².                   (3.47)

3.1.4.7 Определим число трубок в конденсаторе:

N=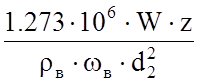,                                                                                 (3.48)

где ρ_в=1000 кг/м³ – плотность охлаждающей воды.

N=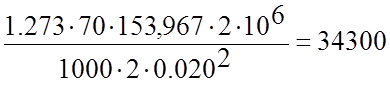шт.

3.1.4.8 Активная длина трубок:

L=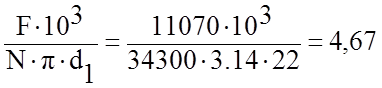м.                                                     (3.49)

3.1.4.9 Удельная паровая нагрузка на конденсатор:

g_п=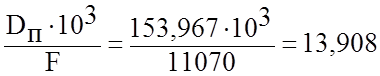г/(м²∙с).                                           (3.50)

Полученная по расчету удельная паровая нагрузка конденсатора близко совпадает с первоначально заданной, и поэтому можно считать расчет законченным и не требующим повторения.

3.1.5 Исходя из выше изложенного внесем следующие изменения в исходные данные расчета по определению площади охлаждения конденсатора и произведем четвертый расчет:

m = 74 – кратность циркуляции;

d₁ = 18 мм – наружный диаметр трубок;

d₂ = 16 мм – внутренний диаметр трубок;

g_п = 14,6 г/(м² с) – предварительно заданная удельная паровая нагрузка;