Определение теплопроводности воздуха методом нагретой нити при атмосферном давлении в интервале температур от 50°C до 250°C (Лабораторная работа № 3)

Министерство Образования Российской Федерации

Филиал ГОУВПО

«Московский энергетический институт

(технический университет)»

в г.Волжском

Кафедра Промышленной теплоэнергетики

Лабораторная работа №3

по курсу теплопередачи

Определение теплопроводности воздуха методом нагретой нити при атмосферном давлении в интервале температур от 50°C до 250°C

Студент                                                                                       Парасоцкий А.Б.

Группа                                                                                         АТП-02

Преподаватель                                                                            Шевцова С.Б.

Волжский 2004

1.  Цель работы

Экспериментальное определение коэффициента теплопроводности воздуха, находящегося вблизи нагретой электрическим током нити.

2. Содержание работы

Проведение опыта. Заполнение таблицы. Анализ полученных результатов. Построение графика зависимости , провести аппроксимирующую кривую  и определить . Определить коэффициент теплопроводности.

3. Теоретические основы работы

          Теплопроводность - один из видов переноса теплоты от более нагретых частей тела к менее нагретым. Обычно этот процесс приводит к выравниванию температуры. Если поддерживать разность температур неизменной, получаем так называемый стационарный процесс. Для стационарного одномерного процесса (температура тела меняется лишь по оси OX) имеем уравнение Фурье:

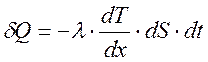,                                                  (3.1)

где      - количество теплоты, переносимое за время  через , нормальную к оси OX, в направлении убывания температуры;

 - градиент температуры;

 - коэффициент теплопроводности.

          При теплопроводности перенос энергии осуществляется в результате непосредственной передачи энергии от молекул, обладающих большей энергией, к молекулам, обладающих меньшей энергией. При малых значениях градиента температуры (), если температура меняется на расстоянии порядка длины свободного пробега молекулы, коэффициент теплопроводности не зависит от градиента температуры, а зависит лишь от агрегатного состояния вещества, его атомно-молекулярного строения, температуры, давления.

Из молекулярно-кинетической теории идеального газа следует, что теоретическое значение коэффициента теплопроводности может быть рассчитано по формуле:

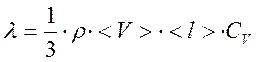,                                            (3.2)

 - плотность газа;

 - средняя статистическая скорость беспорядочного теплового движения молекул;

 - средняя длина свободного пробега молекул;

 - удельная теплоёмкость газа при постоянном объёме.

          Для идеального газа имеем соотношения:

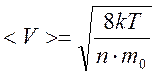        и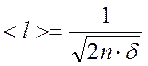       

 - масса молекулы;

 - постоянная Больцмана;

 - число молекул в единице объёма;

 - эффективное сечение столкновения молекул, из (3.2) получим:

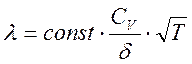,                                           (3.3)

          Отметим, что для реальных газов коэффициент теплопроводности с увеличением температуры растёт быстрее, чем следует из (3.3). Это связано с незначительным увеличением  и уменьшением эффективного сечения столкновений  с ростом температуры. Из опытов следует, что для многих газов (в частности, для воздуха):

,                                                  (3.4)

где .

4. Описание установки и вывод расчётных формул

Нагреваемая вольфрамовая нить (поз.1) протянута по оси симметрии цилиндрического стеклянного баллона (поз.2) с двойными стенками; между стенками залита вода.

Температура воды в баллоне (поз.2) и, следовательно, температура стенки () трубки (поз.З) постоянна в течение опыта. Баллон с нитью закреплён в лабораторном модуле (поз.З). Вольфрамовая нить (поз.1) через гнёзда и соединительные провода подключается к источнику питания постоянного тока приборного модуля. Напряжение на нити  измеряется вольтметром, вмонтированным в приборный модуль (поз.4). Заданное напряжение  выставляется на вольтметре (поз.7) за счёт регулировки рычагов грубой и точной настройки. Ток на нити определяется по падению напряжения  на заданном образцовом сопротивлении . Величина  измеряется милливольтметром (поз.8), подключённым к гнёздам на приборном модуле и к гнёздам на лабораторном модуле, с помощью соединительных проводов при соответствующем положении переключателя (поз.6).

СХЕМА УСТАНОВКИ

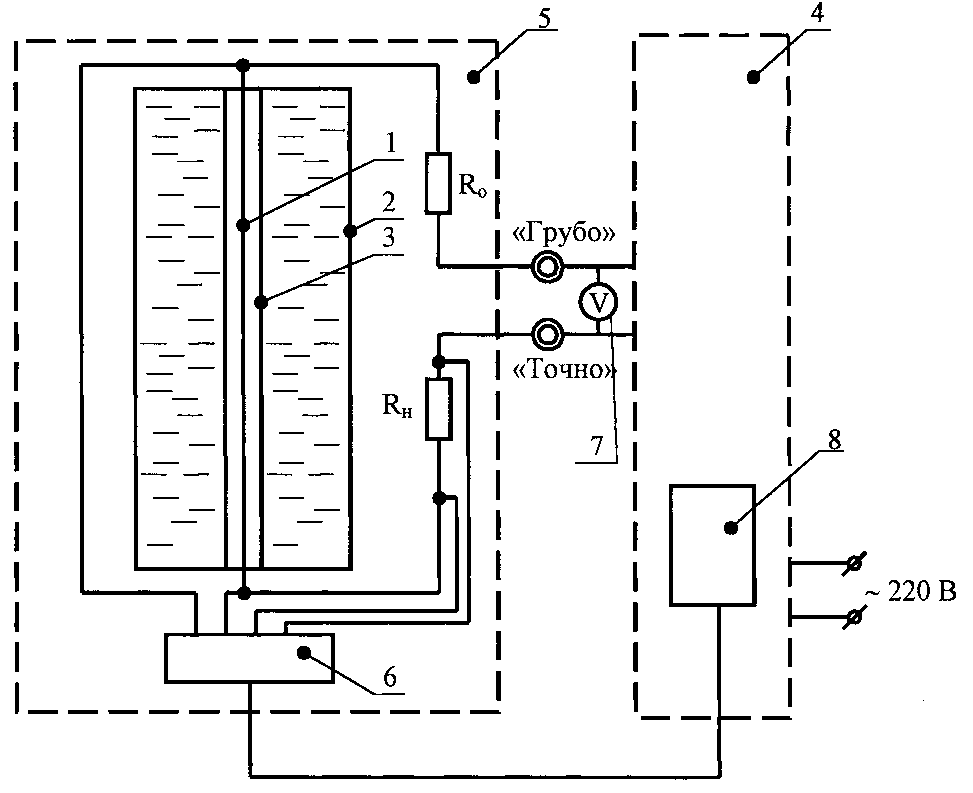
Рис.1

1.  Вольфрамовая нить.

2.  Баллон с двойными стенками.

3.  Трубка.

4.  Приборный модуль.

5.  Лабораторный модуль.

6.  Переключатель.

7.  Вольтметр.

8.  Милливольтметр.

При нагревании нити вдоль радиуса трубки создаётся градиент температуры . Площадь, через которую передаётся тепло, равна площади поверхности цилиндра, коаксиального с нагретой нитью: . При этом соотношение (3.1) принимает вид:

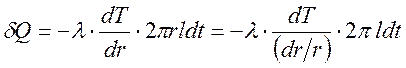,                                (4.5)

 - длина цилиндра;

 - радиус произволен.

Учитывая, что , запишем соотношение (4.5) для мощности теплового потока через поверхность цилиндра

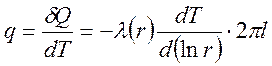,                                         (4.6)

то есть коэффициент теплопроводности зависит от .