Сумма баллов в каждом вертикальном столбце, выраженная в % от суммы всех баллов в таблице, равна весомости выходной характеристики (строка вверху). Например, на рис. 2 входными характеристиками являются Cons_i, и входные данные расположены в столбце B ; выходными характеристиками являются Good_j , а выходные данные находятся в строке 18. Далее, выходные данные таблицы 1 (рис. 2) являются входными данными для таблицы 2 (рис. 3) и т.д. Выходные данные четвертого «Дома» (рис. 5) являются весовыми коэффициентами, определяющими относительную важность мер по улучшению качества, разработанных по QFD - методологии.
Предположим, что этот результат заметно отличается от экспертных оценок, сделанных руководителем на основании опыта (строка 17, рис. 5, 6, 7) . Варьируя нечеткие параметры, определяющие силу связей, можно уменьшить эту разницу. Поскольку на результат влияют только взаимные отношения параметров, один из них - 1 следует оставить неизменным. Два других - 3 и 9 будем варьировать так, чтобы сохранялись исходные качественные различия между параметрами (второй существенно больше первого, а третий существенно больше второго). В остальном выбор произволен, включая, например, наборы значений ( 1, 10 , 100 ) и ( 1, 1.5, 2) .
Используя функции Excel (главное меню - сервис – подбор параметров) осуществляется автоматический подбор значений ячеек с именами коэф1 и коэф2, содержащих настраиваемые параметры (первоначально - 3, 9). Поскольку мы использовали в матрицах связей ссылки коэф1 и коэф2, то при изменении значений ячеек коэф1, коэф2 автоматически пересчитывались все четыре таблицы. Соответственно, изменялись выходные данные так, чтобы их среднеквадратическое отклонение от экспертных оценок весов уменьшилось до уровня, задаваемого в окне подбора параметров (рис. 5, 6, 7 ). Повторяя процедуру можно последовательно уменьшать среднеквадратическое
отклонение ( ячейка I18 ), осуществляя его минимизацию методом покоординатного спуска в плоскости параметров, начиная от точки (3, 9). Очевидно, что нельзя ожидать существенного уменьшения отклонений в значения шести выходных весов (задающих значимости управляющих решений Impr_1 , … , Impr_6 ), варьируя только два параметра. Однако, численные эксперименты с «Домами качества», содержащими от 2-х до 4-х выходных весов (в последней - 4-й таблице) показали следующее. При условии, что настраиваемые параметры не выходят из промежутков [2 ; 4] и [ 8 ; 12 ], а среднеквадратическое отклонение не превышает 15 % от наибольшего из весов, за малое число итераций ( 2 - 10 ) его легко уменьшить на 40 - 90 % . Допуская больший размах варьирования параметров, например в промежутках [2 ; 10] и [20 ; 100], можно существенно увеличить среднеквадратическое отклонение, которое допускает значительное уменьшение при настройке.
При большем числе выходных весов ( 5, 6 и т.д.) следует варьировать параметры по отдельности - для двух, трех или каждой из четырех расчетных таблиц «Дома качества». Таким образом, общее число настраиваемых параметров можно довести до 8. Такого рода настройку, когда покоординатный спуск осуществляется в 8 - мерном пространстве нечетких параметров, по-видимому, целесообразнее запрограммировать средствами VBA пакета Excel.
§ 3. Заключение.
Предложенный метод
настройки нечетких параметров QFD –
методологии, определяющих силу связей в расчетных таблицах, позволяет минимизировать
расхождения с прямыми экспертными оценками. Если эти расхождения малы, то
результат достигается за счет малого удаления параметров от исходных значений.
Если расхождения велики, то настроенные значения могут значительно отличаться
от исходных. В любом случае достигается более адекватное моделирование системы
взглядов и предпочтений экспертов, что отвечает главной задаче теории качеств [5].
За счет этого, при сохранении существа дела и всех достоинств QFD-методологии,
можно сгладить вероятный конфликт с прямыми экспертными оценками приоритетностей
(весов). Если число весов на выходе «Дома качества» велико (![]() ), то предложенный метод практически бесполезен.
Однако, в этом случае руководителю или экспертам будет сложно дать прямые оценки
весов, поэтому возникновение обсуждаемой проблемы маловероятно.
), то предложенный метод практически бесполезен.
Однако, в этом случае руководителю или экспертам будет сложно дать прямые оценки
весов, поэтому возникновение обсуждаемой проблемы маловероятно.
Важно заметить, что игнорирование конфликта оценок может привести к одному из двух нежелательных последствий:
1. Игнорирование интуиции и опыта руководителя ( экспертов ).
2. Потеря доверия руководителя к оценкам, полученным с помощью QFD.
Ссылки :
1. Hauser J.R., Clausing D. The House of Quality // Harvard Business Review. Boston, 1988. Vol. 66, № 3.
2. О.П. Глудкин, Н.М. Горбунов, А.И. Гуров, Ю.В. Зорин; Под ред. О.П. Глудкина. Всеобщее управление качеством: Учебник для вузов М.: Радио и связь, 1999.
3. Rampersad H.К. Total Quality Management: An Executive Guide to Continuous Improvement. Berlin-Heidelberg: Springer Verlag, 2001.
4. Пономарев С.В., Мищенко С.В., Герасимов Б.И., Трофимов А.В.
Квалиметрия и управление качеством. Инструменты управления качеством: Учебное пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2005.
5. Г.И. Брызгалин, Введение в теорию качеств, ВПИ, Волгоград, 1988.
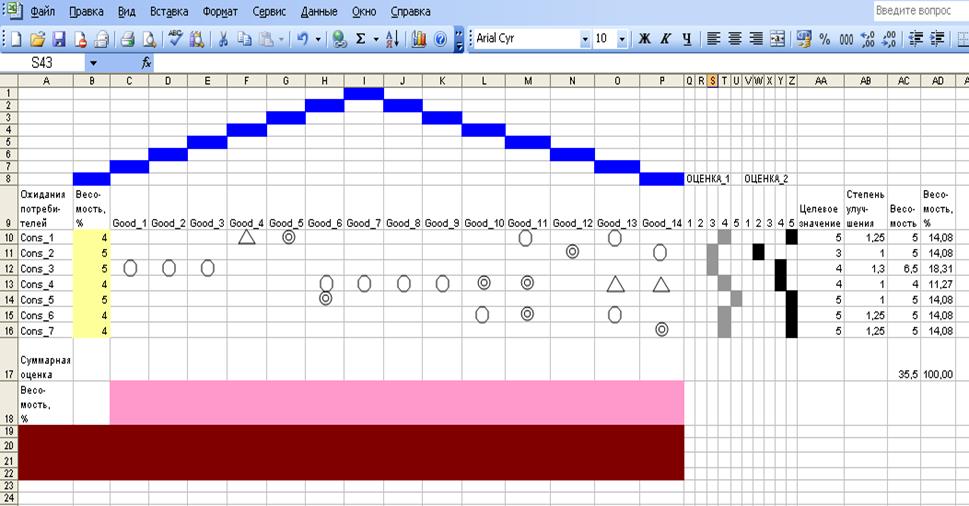
Рисунок 1
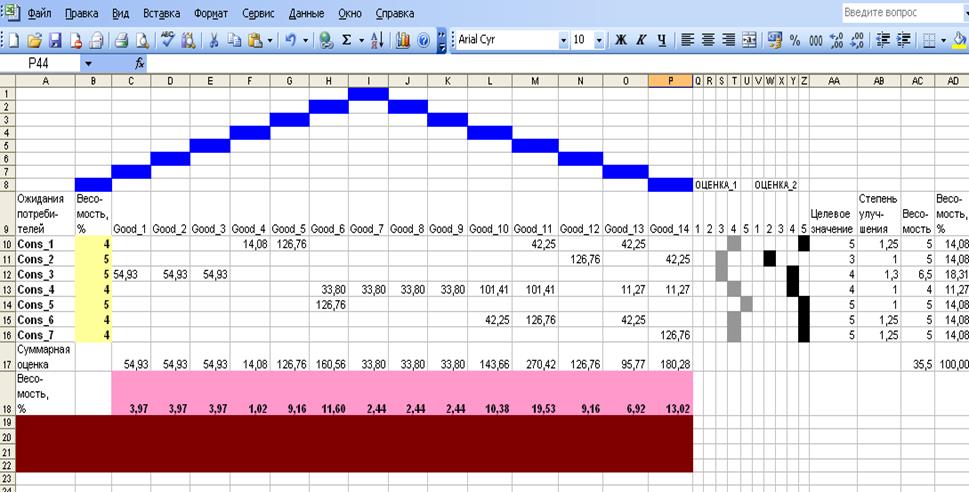
Рисунок 2
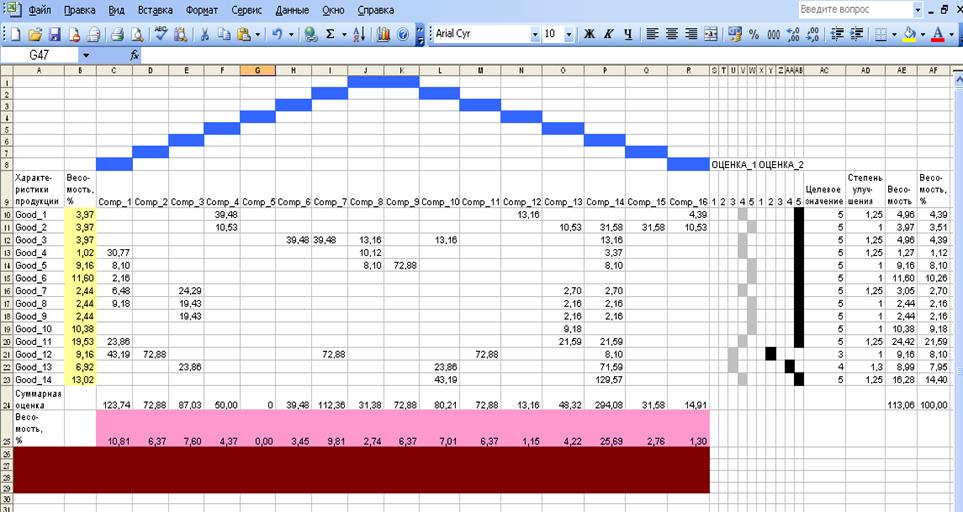
Рисунок 3
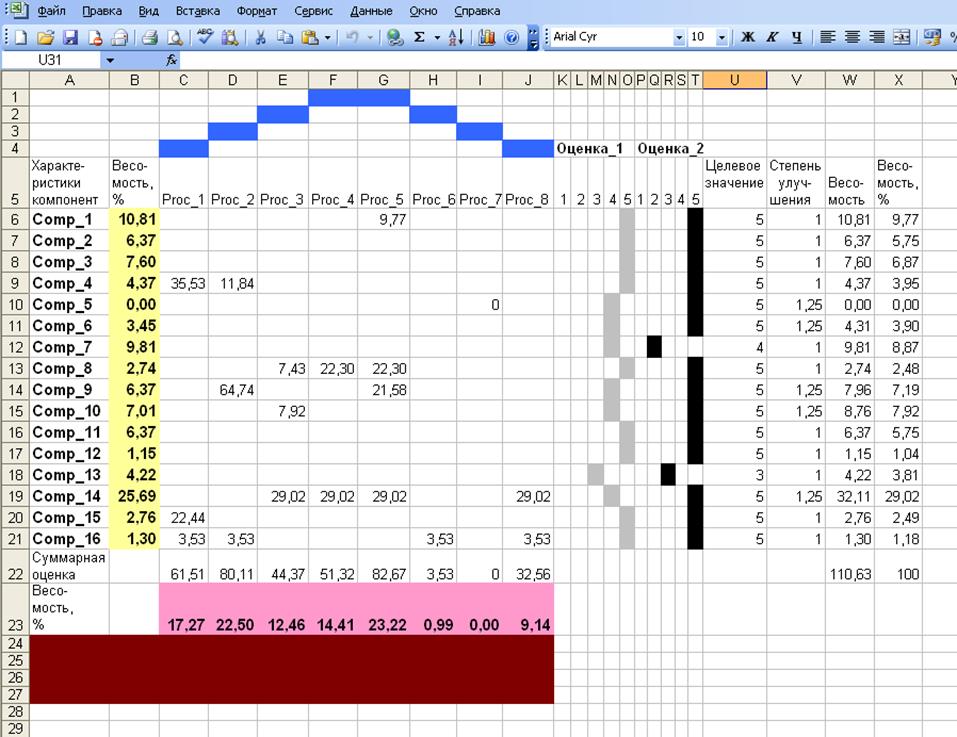
Рисунок 4
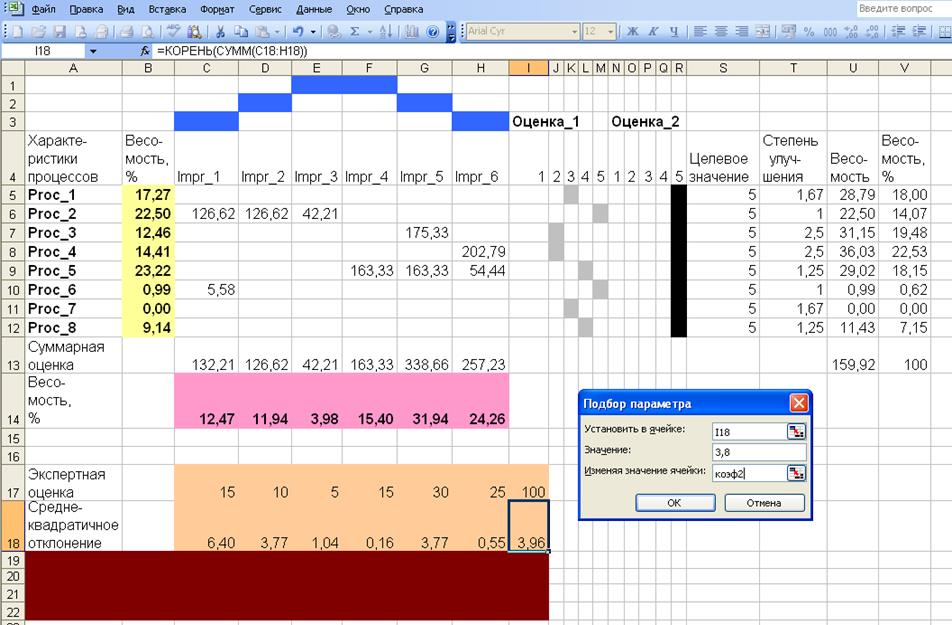
Рисунок 5
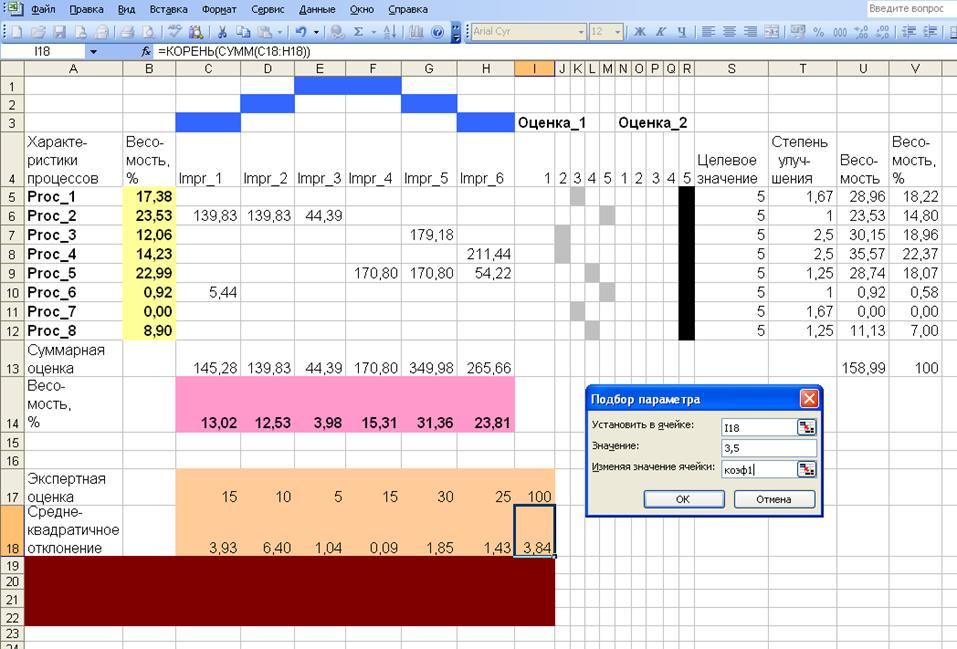
Рисунок 6
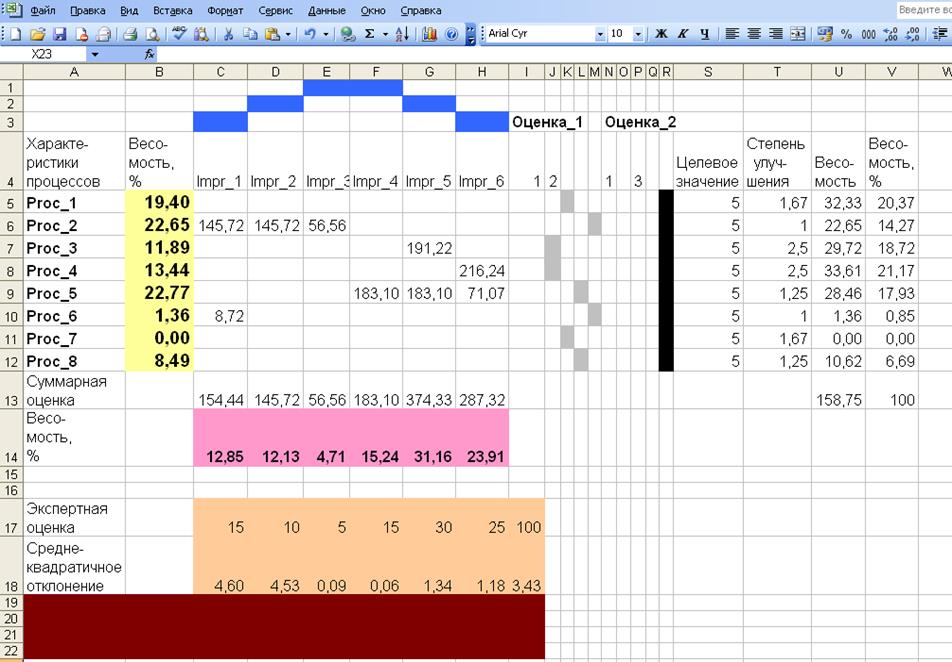
Рисунок 7
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.