Мощностной эффект реактивности, страница 3

Таким образом, минимальная абсолютная погрешность в определении МКР при больших ρ₀ (ρ₀ > 0,3% ∆k/k_эф) составит 2,5*10 ^{– 5} ∆k/k_эф на 1 МВт, или ~ 5% ожидаемого значения. Предпочтительнее малые возмущения, когда приближение точечной кинетики оправдано. Так, при ρ₀ = 5% β_эф = 3,5*10^-2% ∆k/k_эф ∆(МКР) ≈ 10 ^{– 4} или δ(МКР) ≈ 20%, при этом мощность изменится на ~ 50 МВт, а входная температура на ~ 3 ⁰С. При умеренных требованиях к точности измеряемых величин имеется возможность определить МКР с погрешностью не хуже 20%.

Для определения МКР можно использовать и также называемый динамический метод. В этом случае изучается временное поведение реактивности, мощности температуры теплоносителя на входе в реактор и других технологических параметров, влияющих на реактивность, после введения в реактор возмущения реактивности. Поясним суть динамического метода для случая, когда при введении малого возмущения реактивности на реактивность влияют только мощность и температура теплоносителя на входе в реактор. Такое приближение оказывается весьма хорошим для реактора на быстрых нейтронах.

Если в момент t = 0 в реакторе скачком изменилась реактивность, то изменение реактивности во времени при t > 0 можно записать в следующем общем виде:

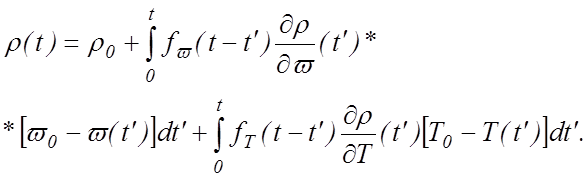                              (12.27)

Функции ƒ_ω(t) и ƒ_Т (t) называют передаточными. Передаточные функции учитывают затяжной во времени характер изменения реактивности при скачкообразном изменении мощности или температуры. Действительно, если мгновенно изменилась мощность, то соответствующее изменение реактивности произойдет не сразу. Необходимо время, чтобы тепло от топлива передалось теплоносителю и конструкциям реактора.

Известны различные математические модели для передаточных функций. В некоторых случаях, когда изменения мощности происходят очень медленно по сравнению с переходными процессами, передаточные функции можно представить в виде δ-функций, и тогда соотношение (12.27) имеет очень простой вид

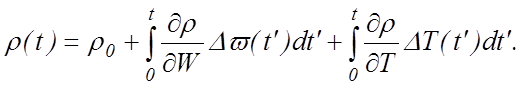                                       (12.28)

В области малых возмущений  ∂ρ/∂ω и ∂ρ/∂Т можно читать постоянными величинами, и тогда по измеренным зависимостям ρ(t), ∆ω(t) и ∆ Т(t) можно найти ТКР(∂ρ/∂Т), МКР(∂ρ/∂ω) и ρ₀, если известны функции ƒ_ω(t) и ƒ_Т (t).

Уравнение (12.27) можно представить в следующей линейной форме:

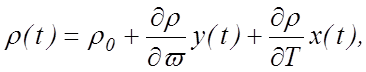                                                             (12.29)

где

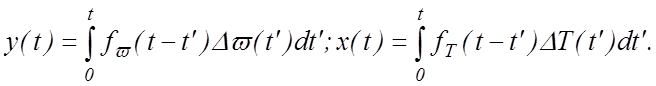
В определенные моменты времени t_i изменяются ρ(t_i), ∆ω(t_i) и ∆ Т(t_i), что позволяет вычислить y(t_i) и х(t_i). Таким образом получается переопределенная система линейных уравнений

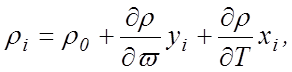                                                                                (12.30)

которую можно решить, используя метод наименьших квадратов для нахождения ρ₀, ∂ρ/∂W и ∂ρ/∂Т.

В качестве первого приближения можно использовать функции y(t) и х(t) в виде 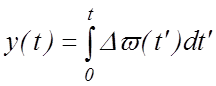 и 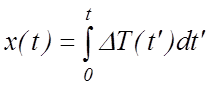. Если найденные в этом приближении ρ₀, ∂ρ/∂ω и ∂ρ/∂Т позволяет в пределах экспериментальных погрешностей описать функцию ρ(t), используя измеренные зависимости ω(t) и Т(t), то это означает, что полученная совокупность экспериментальных результатов с их погрешностями не позволяет уточнить информацию о передаточных функциях.

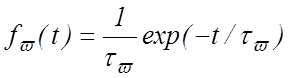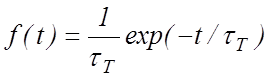Передаточные функции для случая медленно протекающих процессов можно представить в виде  и .Тогда появляется возможность уточнить постоянные τ_ω и τ_Т, используя априорную расчетную информацию о τ_ω и τ_Т и ранее измеренный ТКР.

Рис. 12.6. Зависимость от времени реактивности, мощности, входной (Т_вх) и выходной (Т_вых) температур теплоносителя (при t = 0 в реактор введена положительная реактивность 1,7% β_эф)

На рис. 12.6 приведены типичные зависимости от времени реактивности ρ(t), мощности ω(t), входной и выходной температур теплоносителя после введения в реактор скачком положительной реактивности ~ 1,7% β_эф. Интересно, что в течение примерно первых 200с после введения реактивности входная температура теплоносителя практически не изменяется, что позволяет в этом временном интервале определить МКР. Пример использования динамического метода приведен только с целью, показать возможность извлечения полезной информации из анализа временного поведения технологических параметров реактора при введенных в реактор возмущениях. Отметим, что существует достаточно хорошо разработанное направление исследований – динамика энергетических реакторов со специально разработанным математическим аппаратом и методами изучения нестационарных (переходных) процессов в реакторах [76], которые в данной книге не рассматриваются.