Разработка программы на языке Фортран, осуществляющей интегрирование дифференциальных уравнений с использованием подпрограммы ORK4S1, страница 2

       T=T0+A1(J)

       B=A1(J+1)

       C=A1(J)

       DO 13 I=1,N

       X(I)=X(I)+B*F(I)/3.

   13  AR(I)=X0(I)+C*F(I)

      RETURN

      END

1.5 Результаты

t	y	p	ytoch
0	0	2	0
0,2	0,4	2,04	0,4
0,4	0,82	2,19	0,82
0,6	1,3	2,53	1,3
0,8	1,86	3,31	1,86
1	2,7	5,27	2,7
1,2	4,24	11,64	4,24
1,4	9,22	53,81	9,22

1.6 Графики

Графики точного решения и результата программы совпадают:

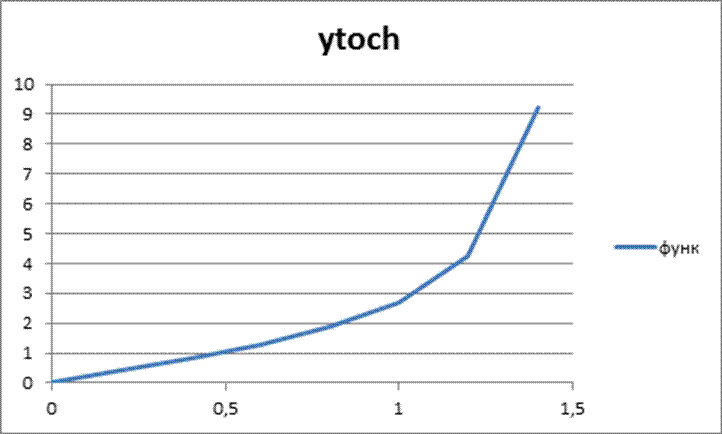
1.7 Вывод

При заданном шаге интегрирования 0.01 осуществляется сходимость.

2. Задание №2

2.1 Задание

Разработать программу на языке Фортран, реализующую заданный метод одномерного поиска и определить с помощью этой подпрограммы экстремум заданной тестовой функции. 

Построить точечный график тестовой функции в EXCEL (не зависимо от результатов расчета программы).

Определить точность найденного экстремума.

2.2 Исходные данные

1) Исходная функция: вариант 11

2) Интервал

[0, 1]

3) Метод №2: дихотомии

2.3 Таблица идентификаторов.

a – левая граница интервала

b – правая граница интервала

eps – точность получаемого решения, условие окончания поиска

delta ­─ 0 < δ < (b-a)/2

xmin – аргумент точки экстремума

fmin – значение аргумента в точке экстремума

numb – номер итерации

2.4  Описание подпрограмм

1. Подпрограмма общего типа dihotomy(a,b,eps,delta,xmin,fmin)

 Подпрограмма определяет аргумент  точки экстремума

2. Подпрограмма  fun(x)

Предназначена для вычисления значения данной функции. Подпрограмма типа function.

2.5 Текст подпрограммы:

2.5.1 Текст подпрограммы общего типа dihotomy(a,b,eps,delta,xmin,fmin)

      Subroutine dihotomy(a,b,eps,delta,xmin,fmin)

      integer numb

      real a,b,eps,delta,xmin,fmin

      open(10,file='result.txt')

      write(10,2)

      a1=a

      b1=b

              numb=0

      delta1=Delta

      do while(abs(a1-b1)>eps)

      deltakon=Delta1

              numb=numb+1

      akon=a1

      bkon=b1

      x1=a1+(b1-a1)/2-delta1

      x2=a1+(b1-a1)/2+Delta1 

      func1=fun(x1)

      func2=fun(x2)

            if (func1<func2) then

      b1=x2

      xmin=x1

      fmin=fun(x1)

      else

      a1=x1

      xmin=x2

      fmin=fun(x2)

      end if

      delta1=Delta1/2

              write(10,3) numb,akon,bkon,deltakon,x1,x2,func1,func2,xmin,fmin

2     format(1x,'numb',5x,'a1',7x,'b1',7x,'delta1',5x,'x1',5x,

     *'x2',5x,'func1',4x,'func2',4x,'xmin',4x,'fmin')

3     format(i3.0,1x,f7.4,1x,f7.4,1x,1x,f9.7,1x,f7.4,1x,f7.4,1x

     *,1x,f7.4,1x,1x,f7.4,1x,f7.4,1x,1x,f7.4,1x) 

      end do

      end

2.5.2 Текстподпрограммы  fun(x)

      Function fun(X)

      real x

      fun=x**2+1.5*exp(-X)

      end

2.5.3 Текст главной программы

Program main

call dihotomy(0.,1.,0.001,0.01,xmin,fmin)

print *,xmin,fmin

end

2.6 Результаты:

numb	a1	b1	delta1	x1	x2	func1	func2	xmin	fmin
1	0	1	0,01	0,49	0,51	1,159	1,1608	0,49	1,159
2	0	0,51	0,005	0,25	0,26	1,2307	1,12242	0,26	1,2242
3	0,25	0,51	0,0025	0,1275	0,1325	1,1709	1,1695	0,3825	1,1695
4	0,3775	0,51	0,00125	0,065	0,0675	1,1594	1,1593	0,445	1,1593
5	0,4425	0,51	0,000625	0,0331	0,0344	1,1585	1,1585	0,4756	1,1585

2.7 Вывод

Разработанная программа для данного примера достигает необходимой точности решения 0.001 за 5 итераций.

2.9 График точной функции:

0	1,5
0,1	1,367256
0,2	1,268096
0,3	1,201227
0,4	1,16548
0,5	1,159796
0,6	1,183217
0,7	1,234878
0,8	1,313993
0,9	1,419854
1	1,551819