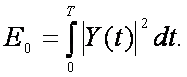Устройство формирования сигналов системы связи с кодовым уплотнением каналов: Дипломный проект, страница 2

                                           (6.1)

Оптимальным  обнаружителем  в  этом  случае,  будет энергетический приемник. Время обнаружения [3], Тоб определяется из выражения:

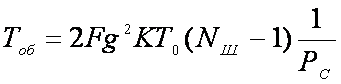                         (6.2)

где: g - отношение сигнал шум на входе приемника.

       К = 1.38*10^-23 - постоянная Больцмана.

       Т₀ = 300 К, температура по шкале Кельвина.

       Nш- спектральная плотность шума.

       Рс - мощность сигнала.

       F - ширина спектра сигнала.

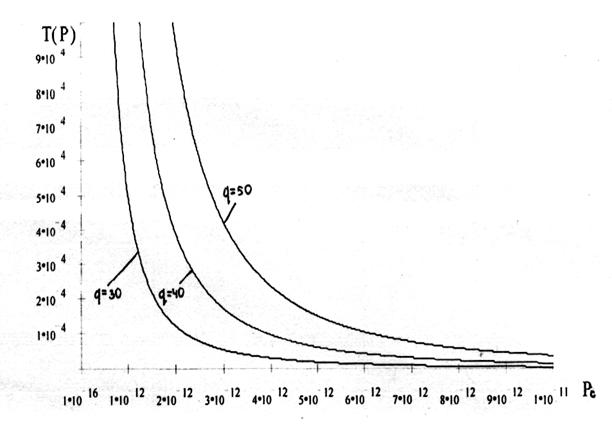
Графические зависимости времени обнаружения от отношения сигнал - шум и мощности сигнала на входе приемника показаны на рисунках 6.1, 6.2.

Рисунок 6.1 - Зависимость времени обнаружения от отношения сигнал/шум

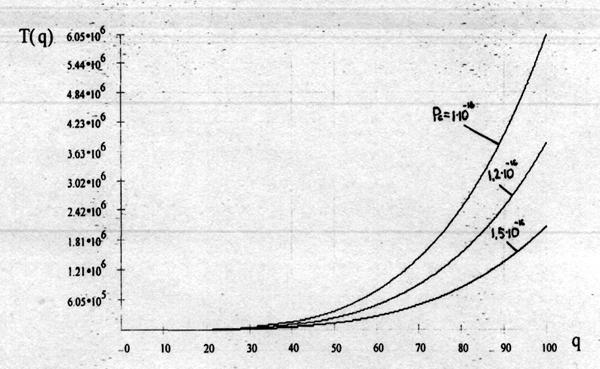         Рисунок 6.2 - Зависимости       времени         обнаружения       от                                      мощности сигнала на входе приемника

         Характеристики обнаружения рассчитаем по методике изложенной в [3]. В соответствии с этой методикой вероятность ложной тревоги выражается следующей формулой

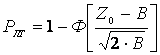                                            (6.3)

где  Ф[z] - интеграл вероятности или функция Лапласа;

        z₀ - пороговый уровень;

         В - величина базы сигнала.

Вероятность правильного обнаружения задается следующей формулой

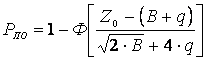                                            (6.4)

где q - отношение сигнал/помеха на входе энергетического приемника.

         Как видно из приведенных формул, в том случае когда В ›› q, то Рп.о. = Рл.т.. Это лишний раз подчеркивает тот факт, что для сигналов с большой базой при небольших отношениях сигнал/помеха на входе энергетического приемника обеспечивается высокая скрытность работы системы связи.

         Для построения характеристик обнаружения энергетического разведприемника зададимся вероятностью ложной тревоги равной Рл.т. =10^-4, что по критерию идеального наблюдателя соответствует такой же вероятности и для пропуска сигнала (ошибочность приема).

         При заданной Ρл.т. найдем значение пороговой величины Z₀ следующим образом: по таблице значений функции Лапласа находим аргумент z, при котором Ф[z] = 0,9999. Этот аргумент составляет z = 2,8. Следовательно, при Φ[z] - 0,9999 вероятность ложной тревоги будет Рл.т. = 10^-4, так как 1 - 0,9999 = 10^-4

         Задавшись теперь значением базы B=F*T=50, найдем условную величину порога Z₀ следующим образом

                                                 (6.5)

         Выражая Z₀ из (6.5), получим Z₀ = 78. Подставляя значения Z₀ в формулу (6.4) и придавая отношению сигнал/помеха различные значения строим характеристику обнаружения энергетического приемника.

         Нетрудно видеть из формулы (6.4), что вероятность правильного обнаружения будет равна единицы в том случае, когда сумма значений базы и отношения сигнал/помеха будет равна пороговому значению, так как Φ[0] = 0.

         На рисунке 6.3 приведены характеристики обнаружения для значений базы В=2,  В=10,  В=50,  В=100,  В=600,  В=1000,  В=104,  В=106  и Рл.т.=10^-4

Следует отметить, что q характеризует сигнал/помеха в полосе F₀ линейной части разведприемника. Из характеристик обнаружения видно, что увеличение базы В приводит к уменьшению вероятности правильного обнаружения при прочих равных условиях. Это значит, что скрытность работ