Модуляция и демодуляция сигналов, страница 2

Рис. 3. Временной и частотный спектры ФМ колебания

Имитация канала связи

Функция awgn реализует канал связи с аддитивным белым гауссовым шумом, т.е. добавляющая к сигналу белый шум с заданным уровнем. Результатом работы является вектор «зашумленных» отсчетов. Если значения функции являются вещественными, функция awgn добавляет вещественный шум, если комплексными - комплексный. Получим аддитивную смесь сигнала с шумом и построим его спектр:

ych = awgn(y, 9, 'measured', 'dB');      % добавление белого шума с ОСШ=9 дБ к сигналу

subplot(6,2,5);

plot(t1,ych);     %график зашумленного сигнала

grid on;

n1=length(t1);                                

a3=fft(ych);                                        

F1=(0:n1-1)/n1*Fs;                                  

a3=abs(a3);

subplot(6, 2, 6);

stem(F1(1:length(F1)/2), a3(1:length(F1)/2),'.');

grid on;

Графики на рис. 4.

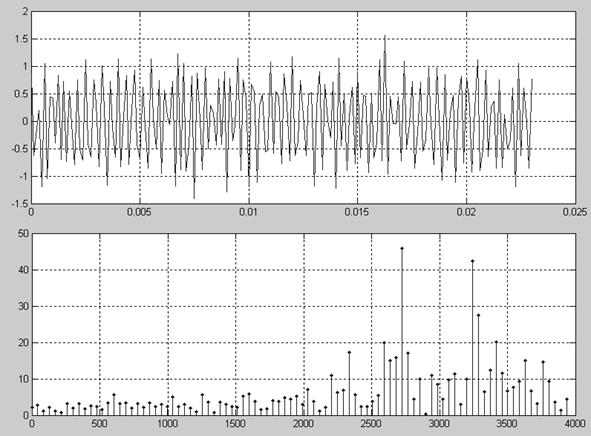
Рис. 4. Временной и частотный спектры аддитивной смеси

Предварительная фильтрация сигнала на входе приемника

Необходимо синтезировать полосовой фильтр отвечающий следующим требованиям:

1.  Как можно большее подавление вне полосы пропускания.

2.  Как можно меньшие амплитудные и фазовые искажения в полосе пропускания.

В нашем случае полоса пропускания будет от 2 до 4 КГц (см. рис. 3 и рис. 4). Оптимальным для данных условий будет ПФ Чебышева 1-го рода с уровнем пульсаций в полосе пропускания не более 1 дБ. Выполним фильтрацию и построим спектр сигнала на выходе:

w1=2150*2/Fs;

w2=3900*2/Fs;

[b1,a10] = cheby1(8,1,[w1 w2]);            % Bandpass Chebyshev Type I

yfilt=filter(b1, a10, ych);

subplot(6,2,7);

plot(t1,yfilt);

grid on;

n1=length(t1);                                              

a4=fft(yfilt);                                        

F1=(0:n1-1)/n1*Fs;                                  

a4=abs(a4);

subplot(6, 2, 8);

stem(F1(1:length(F1)/2), a4(1:length(F1)/2),'.'); 

grid on;

Полученные зависимости на рис. 5.

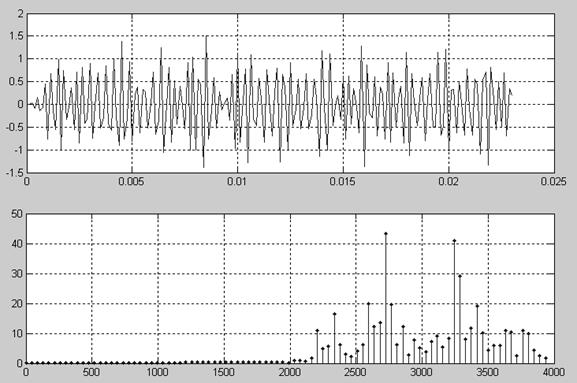
Рис. 5. Временной и частотный спектры аддитивной смеси после фильтра

Демодуляция сигнала

Демодуляция ФМ-сигнала производится путем формирования аналитического сигнала с помощью функции Hilbert, сдвига его спектра в область нулевых частот путем умножения на exp(-j2πFct) и выделения фазового угла. Результат делится на beta. При демодуляции параметр beta по умолчанию равен единице.

xdem=demod(yfilt,Fc,Fs,'pm',k);                       % демодуляция

subplot(6,2,9);

plot(t1,xdem);

grid on;

n1=length(t1);        

a5=fft(xdem);

F1=(0:n1-1)/n1*Fs;

a5=abs(a5);

subplot(6, 2, 10);

stem(F1(1:length(F1)/2), a5(1:length(F1)/2),'.');

grid on;

Графики на рис. 6.

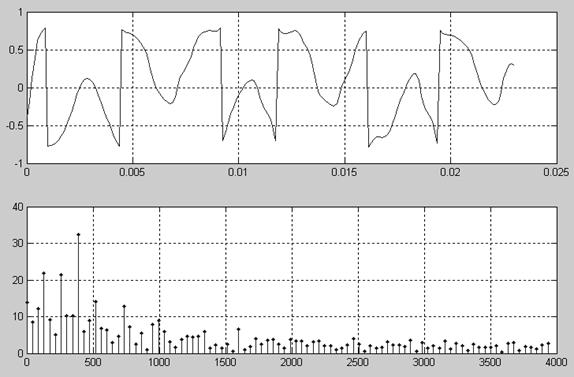
Рис. 6. Временной и частотный спектры демодулированного сигнала

«Очищение» спектра демодулированного сигнала

В результате выполнения этой операции сигнал после демодуляции должен в точности повторить исходный (переданный) сигнал. Но в связи с тем, что практически невозможно выделить спектр полезного сигнала и сохранить фазовые соотношения, нужно искать оптимальные пути преобразования. Также следует учитывать, что многократная фильтрация существенно ослабляет сигнал и уменьшает ОСШ. В нашем случае важнее всего отсеять высокочастотные составляющие. Для этого синтезируем ФНЧ (пусть Баттерворта) с частотой среза чуть менее частоты 3-й гармоники сигнала (для того, чтобы частично ослабить ее по отношению к 1-й):