Исследование генераторов псевдослучайных последовательностей

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Таганрогский Технологический институт

Южного Федерального университета

Лабораторная работа №1

по курсу БЖ

«Исследование генераторов

псевдослучайных последовательностей»

Выполнил:

Рудь Д. Е.

Проверил:

Шеболков В. В.

Таганрог 2008

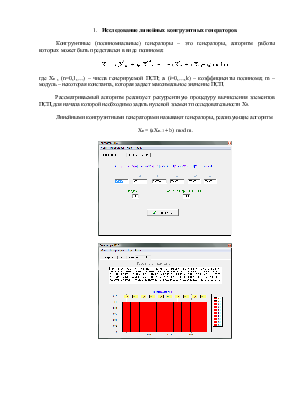
1.  Исследование линейных конгруэнтных генераторов

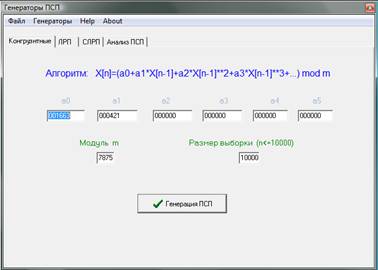
Конгруэнтные (полиномиальные) генераторы – это генераторы, алгоритм работы которых может быть представлен в виде полинома:

где Xn , (n=0,1,…) – числа генерируемой ПСП; ai (i=0,…,k) – коэффициенты полинома; m – модуль – некоторая константа, которая задает максимальное значение ПСП.

Рассматриваемый алгоритм реализует рекуррентную процедуру вычисления элементов ПСП, для начала которой необходимо задать нулевой элемент последовательности X0.

Линейными конгруэнтными генераторами называют генераторы, реализующие алгоритм

Xn = (aXn-1 + b) mod m.

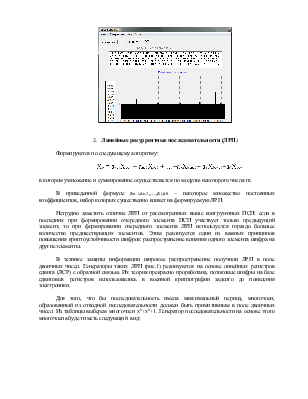
2.  Линейные рекуррентные последовательности (ЛРП)

Формируются по следующему алгоритму:

в котором умножение и суммирование осуществляется по модулю некоторого числа m.

В приведенной формуле an-1,an-2,…,a1,a0 – некоторое множество постоянных коэффициентов, набор которых существенно влияет на формируемую ЛРП.

Нетрудно заметить отличие ЛРП от рассмотренных выше конгруэнтных ПСП: если в последних при формировании очередного элемента ПСП участвует только предыдущий элемент, то при формировании очередного элемента ЛРП используется гораздо большее количество предшествующих элементов. Этим реализуется один из важных принципов повышения криптоустойчивости шифров: распространение влияния одного элемента шифра на другие элементы.

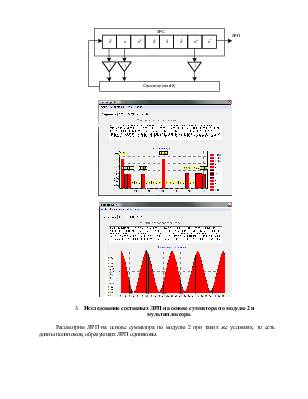
В технике защиты информации широкое распространение получили ЛРП в поле двоичных чисел. Генераторы таких ЛРП (рис.1) реализуются на основе линейных регистров сдвига (ЛСР) с обратной связью. Их теория прекрасно проработана, потоковые шифры на базе сдвиговых регистров использовались в военной криптографии задолго до появления электроники.

Для того, что бы последовательность имела максимальный период, многочлен, образованный из отводной последовательности должен быть примитивным в поле двоичных чисел. Из таблицы выберем многочлен х⁶+х¹+1. Генератор последовательности на основе этого многочлена будет иметь следующий  вид:

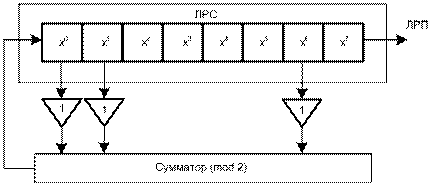
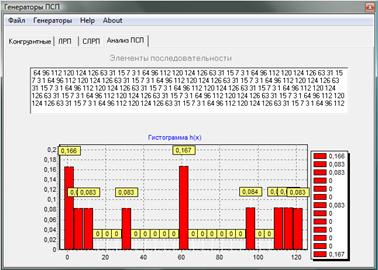
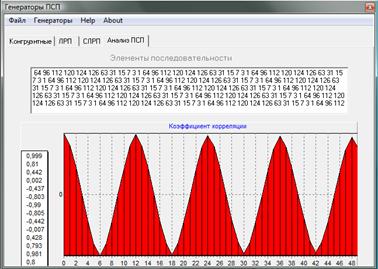
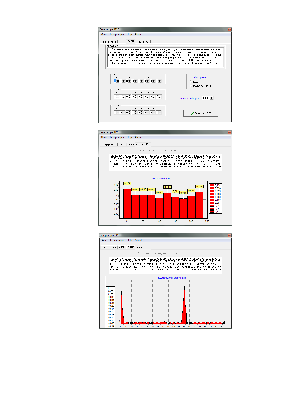
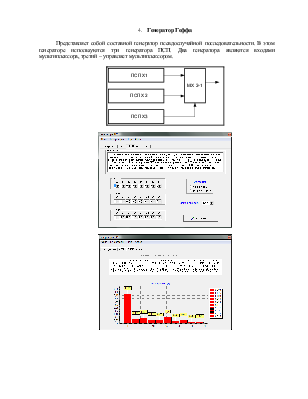
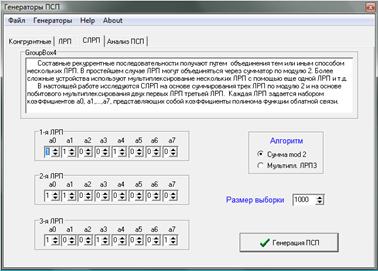
3.  Исследование составных ЛРП на основе сумматора по модулю 2 и мультиплексора.

Рассмотрим ЛРП на основе сумматора по модулю 2 при таких же условиях, то есть длины полиномов, образующих ЛРП одинаковы.