Тест на 4 бали з дисципліни "Системи та методи прийняття рішень" (Діапазон робочої області визначення функції КФЕ)

Тести на 4  (СМПР, Шелехов)

1. Дано  радіус та масив кодових відстаней. Розрахувати помилку першого та другого роду, першу та другу достовірність.

К1=6, к2=4, к3=8, к4=2.

Помилка першого та другого роду: α=k2/n=4/10=0,4; β=k3/n=8/10=0,8

Перша та друга достовірність: D1= k1/n=6/10=0,6; D2= k4/n=2/10=0,2

2.   Вказати діапазон робочої області визначення функції  КФЕ :

d	1	2	3	4	5	6	7	8
D1	0.01	0.49	0.58	0.7	0.89	0.91	1	1
D2	1	1	0.61	0.4	0.39	0.19	0.1	0

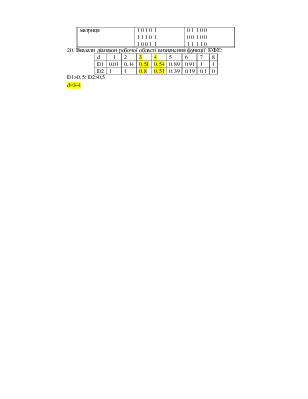
D1>0,5; D2>0,5

d=3

3. Дано навчальну матрицю для синтезу СППР за МФСВ. Побудуйте бінарний еталонний вектор.  Крок дельта20, рівень селекції=0.5.  Матриця яскравості:

Знаходимо середнє арифметичне по стовпцям:  18,5; 35; 30; 28,75

Знаходимо контрольні допуски: 18,5+20=28,75; 18,5-20=-1,75

55 – 15; 50 – 10; 48,75 – 8,75

Якщо елем. з матриці яскравості входять в контрольні допуски, то ставимо 1, якщо ні то 0.

0	0	1	1
1	1	1	1
1	0	1	1
1	0	1	0

Будуємо бінарний еталонний вектор, дивлячись на матр.яскравості. EV=[0.75,0.25,1,0.75]=[1,0,1,1] (зрівнюємо з рівнем селекції, якщо > то ставимо 1, якщо < то 0).

4. Дано радіус та масив кодових відстаней. Розрахувати помилку першого та другого роду, першу та другу достовірність.

К1=2, к2=8, к4=8, к4=6. (Порівнюємо з радіусом 3)

Помилка першого та другого роду: α=k2/n=8/10=0,8; β=k3/n=4/10=0,4

Перша та друга достовірність: D1= k1/n=2/10=0,2; D2= k4/n=6/10=0,6

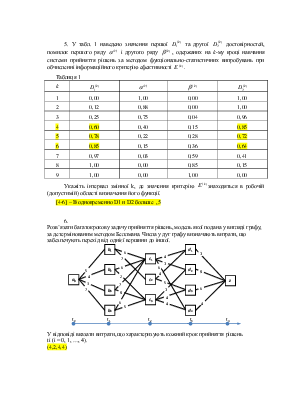
5. У табл. 1 наведено значення першої  та другої  достовірностей, помилок першого ряду  і другого ряду , одержаних на k-му кроці навчання системи прийняття рішень за методом фукціонально-статистичних випробувань при обчисленні інформаційного критерію ефективності .

Таблиця 1

k
1	0,00	1,00	0,00	1,00
2	0,12	0,88	0,00	1,00
3	0,25	0,75	0,04	0,96
4	0,60	0,40	0,15	0,85
5	0,78	0,22	0,28	0,72
6	0,85	0,15	0,36	0,64
7	0,97	0,03	0,59	0,41
8	1,00	0,00	0,85	0,15
9	1,00	0,00	1,00	0,00

Укажіть інтервал змінної k, де значення критерію знаходяться в робочій (допустимій) області визначення його функції.

[4-6] – В одновременно D1 и D2 больше  ,5

6.

Розв’язати багатокрокову задачу прийняття рішень, модель якої подана у вигляді графу, за детермінованим методом Беллмана. Числа у дуг графу визначають витрати, що забезпечують перехід від однієї вершини до іншої.

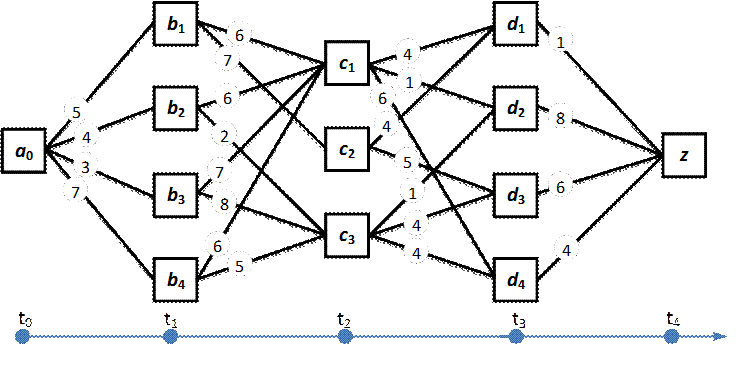
У відповіді вказати витрати, що характеризують кожний крок прийняття рішень

ti (i = 0, 1, …, 4).

(4,2,4,4)

7. Для гіперсферичного класифікатора визначити належність класу розпізнавання , для якого відомі еталонний вектор-реалізація  і оптимальний радіус  ,  таких векторів-реалізацій:

, ,

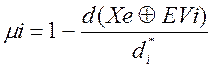
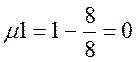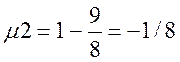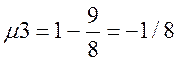
8. Розв’язати задачу вибору найкращої структури обсягу закупівлі оптової компанії продукції для реалізації по торговим підприємствам, використовуючи принцип гарантованого результату, тобто максиміна. Для вибору продукції було сформовано декілька цільових критеріїв: строк зберігання, оптова ціна та асортимент торгової марки. Вибір виробника виконувався з таких підприємств-постачальників: Долина; Топаз; Масандра. Вхідні дані наведені в таблиці

	Масандра	Долина	Топаз
Строк зберігання	3	6	4
Оптова ціна	8	5	2
Асортимент	1	4	5