Средства моделирования. Моделирование аналоговых схем. Моделирование цифровых схем, страница 11

L^@REFDES %1 %2 ?TOLERANCE|L^@REFDES| @VALUE ?IC/IC=@IC/ ?TOLERANCE|\n.model L^@REFDES IND L=1 DEV=@TOLERANCE ?TC1/TC1=@TC1/ ?TC2/TC2=@TC2/ ?IL1/ IL1=@IL1/ ?IL2/ IL2=@IL2/|

Помимо атрибутов уже описанных для резистора и имеющих для конденсатора такое же назначение, в приведенном выше шаблоне добавлены коэффициенты напряжения:

IL1 – линейный коэффициент тока,

IL2 – квадратичный коэффициент тока,

и начальный ток IC через индуктивность учитываемый при расчете по постоянному току .

Индуктивность катушки рассчитывается по формуле:

L=Lном (1+TC1(T–T_MEASURED)+ TC2(T–T_MEASURED)²)´

´(1+IL1·I+IL2·I²)

где I – текущий ток через индуктивность.

2.5  Взаимная индуктивность и магнитный сердечник

Данные компоненты почти не моделируются в EWB для них нужно создавать эквивалентные схемы. Об этом и будет идти речь в лабораторной работе № 4.

В OrCAD для связи между катушками индуктивности может использоваться простая модель взаимной индуктивности или более сложная модель магнитного сердечника.

Взаимная индуктивность имеет следующий шаблон:

Kn^@REFDES L^@L1 ?L2|L^@L2| ?L3|\n+ L^@L3| ?L4|L^@L4| ?L5|\n+ L^@L5| ?L6|L^@L6| @COUPLING

где COUPLING – коэффициент связи равный:

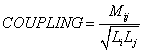
M_ij – взаимная индуктивность катушек L_i и L_j;

В результате получаем идеализированную модель связанных катушек индуктивности. Ток через индуктивность L_i определяется выражением:

Магнитный сердечник имеет следующий шаблон:

Kn^@REFDES L^@L1 ?L2|L^@L2| ?L3|\n+ L^@L3| ?L4|L^@L4| ?L5|\n+ L^@L5| ?L6|L^@L6| @COUPLING &MODEL

Он отличается от шаблона взаимной индуктивности атрибутом MODEL. Однако, если магнитный сердечник имеет свойство Implementation – имя модели, то это в корне меняет вообще модель связанных катушек индуктивности. Индуктивность катушек теперь определяется на основе формулы, связывающей параметры магнитного сердечника и количества витков катушки, т. е. теперь основным параметром катушки считается количество витков, а не собственно индуктивность как это было выше для простой модели взаимной индуктивности. Поэтому на схеме следует указывать вместо L количество витков. Формула для индуктивности известна из электротехники:

где w – количество витков катушки;

m, m₀ – магнитная проницаемость относительная и для вакуума;

S – площадь поперечного сечения магнитопровода (м²);

l_ср – длина средней магнитной силовой линии (м).

Параметру l_ср в списке параметров модели соответствует PATH (см), параметру S – AREA*PACK (см²) (площадь поперечного сечения умножить на коэффициент заполнения). Если есть воздушный зазор, он определяется параметром GAP (см). Однако, зазор должен быть небольшим, что приводит к затруднению моделирования штыревых сердечников. Впрочем, штыревые сердечники используются на высоких частотах, а частотные свойства материала не учитываются. Следовательно, моделирование магнитных сердечников имеет смысл выполнять только на частотах снятия безгистерезисной кривой или близких, а это низкие частоты 50, 60 Гц. На высоких частотах лучше использовать модель индуктивности и взаимной индуктивности.

Магнитная проницаемость вычисляется исходя из параметров безгистерезисной кривой и начальной магнитной проницаемости. Подробно процедура получения зависимости m(H) приведена в [3]. Однако, процедура трудоемка. Если магнитные сердечники из заданного материала присутствуют в библиотеке моделей, то легче воспользоваться параметрами этого сердечника, установив требуемые PATH и AREA. Затем, можно применить какой либо способ измерения индуктивности. Рекомендуется для ориентировочного значения использовать измерение индуктивного сопротивления, пропуская через индуктивность переменный ток. Можно также использовать резонансный способ.