Синтаксичний аналіз. Спадний аналіз. Предиктивний аналізатор. Висхідний аналіз, страница 13

Тепер обчислимо goto(I₀ , X) для різних значень X. Для X = S ми повинні замкнути пункт [S'→ S•, $]. Ніяких інших пунктів у замиканні немає, оскільки точка в пункті знаходиться справа. Таким чином, множина пунктів має вигляд

I₁ :   S'→ S'•, $ .

Для X = С замикаємо [S → C•C, $]. Ми додаємо С-продукції з другим компонентом $ і після цього додати вже нічого. Тим самим одержуємо

I₂ :   S → C•C, $ ,

С→ •сC, $,

С→ •d, $  .

Далі нехай Х= c, і замикається {[ С→ с•C, c|d]}. Додаємо C-продукції з другим компонентом c|d, одержуючи

I₃ :       С→ с•C, c|d ,

С→ • с C, c|d ,

С→ •d, c|d  .

І нарешті, для X=d знаходимо

I₄:С→ d•, c|d .

На цьому ми завершуємо розгляд gotoна множині I₀. Для I₁ нові множині не утворюються, але I₂ має переходи за C, c і d. Для C знаходимо

            I₅ :       С→ CC•, $.

Для c розглядаємо замикання {[С→ с•C, $]}, одержуючи

I₆ :       С→ c•C, $ ;

С→ •c C, $ ;

С→ •d, $  .

Продовжуючи розгляд функції goto для I₂, знаходимо goto (1₂, d):

I₇:С→ d•, $  .

Переходячи до I₃, знайдемо, що переходи з I₃ по символах  с  і dявляють собою відповідно I₃ та I₄, а goto(I₃,C)  –

1₈:           С→ сC•, c|d .

I₄ і I₅переходів не мають. Переходи з 1₆ по символах с і dявляють собою відповідно I₆ та I₇, а goto(1₆,C)–

1₉:      С→ сC•, $ .

Інші множини пунктів не мають переходів, і на цьому наша робота завершена. На рис. 4.7 показані знайдені десять множин пунктів з їх переходами.

Тепер наведемо правила, за допомогою яких на основі множин LR(1)-пунктів будуються функції actionі gotoLR(1)-аналізу. Функції представлені, як і раніше, у вигляді таблиці; відмінність полягає у значеннях записів.

Алгоритм 4.10 Побудова канонічної таблиці LR-аналізу

1 Побудуємо C = {1₀,1₁,..., 1_n}, систему множин LR(1)-пунктів для G'.

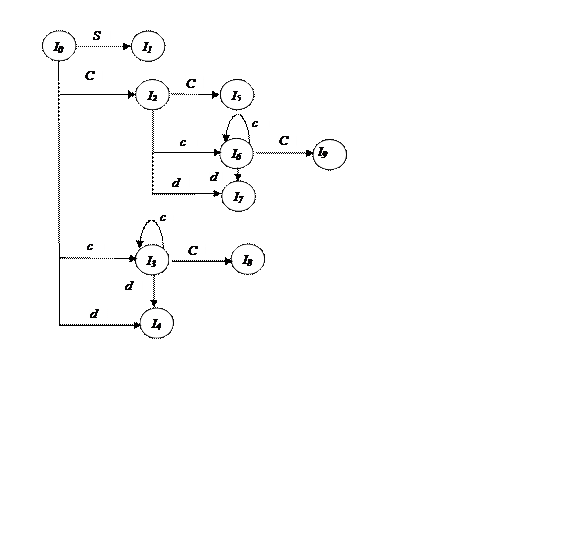
Рисунок 4.7 - Діаграма переходів для граматики 4.6

2 Стан i синтаксичного аналізатора будується на основі множини 1_i. Дії синтаксичного аналізу для стану i визначаються в такий спосіб:

а) якщо   [А→α•aβ, b]I_i і   goto(I_i, а) = I_j ,   то   установимо   action[i, а] таким, що дорівнює “перенесення j”;  

б) якщо [А→α•, a]I_i,  А≠S', то визначимо action[i,a] як “згортання A→α”;

с) якщо [S'→S•, $]I_i, то установимо action[i,$] таким, що дорівнює “допуск”.

Якщо застосування цих правил приводить до конфлікту, граматика не є LR(1)-граматикою, і даний алгоритм до неї незастосовний.

3 Переходи   gotoдля   стану   i   визначаються   в   такий спосіб:   якщо goto(I_i, A) = I_j, то goto[i, А] =j.

4 Усі записи, не визначені правилами (2) і (3), задаються як “помилка”.

5  Початковий стан синтаксичного аналізатора являє собою стан, побудований з множини, що містить пункт [S'→S•, $].

Таблиця, побудована на основі функцій actionі gotoсинтаксичного аналізу, отриманих з використанням даного алгоритму, називається канонічною таблицею LR(1)-аналізу. LR-аналізатор, що використовує цю таблицю, називається канонічним LR(1)-аналізатором. Якщо функція actionсинтаксичного аналізу не має множинних записів, то дана граматика називається LR(1)-граматикою.

Таблиця 4.7

Стан	action	goto
	c            d            $	S              C
0 1 2 3 4 5 6 7 8 9	s3         s4                               acc    s6          s7                      s3          s4    r3         r3                              r1    s6         s7                              r3    r2         r2                              r2	1  2 5                   8                   9

Таблиця 4.7 являє  собою таблицю синтаксичного аналізу для граматики (4.6). Продукціями 1, 2  і  3 є відповідно S→CC, С→ сCіС→ d.

Будь-яка SLR(1)-граматика є LR(1)-граматикою, але для SLR(1)-граматики канонічний LR-аналізатор може мати більше станів, ніж SLR-аналізатор для тієї самої граматики.

Граматика з попереднього прикладу є SLR-граматикою; SLR-аналізатор для неї має сім станів, а в даній таблиці їх десять.

Завдання до розділу 4

1 Побудувати предиктивний синтаксичний аналізатор для граматики

bexpr → bexpr or bterm | bterm

bterm → bterm  and  bfactor | bfactor

bfactor → not bfactor  | (bexpr) | true | false.

2 Побудувати таблицю SLR-аналізу для граматики

E→E+T | T ;

T→TF | F;

F→F* | a | b .

3  Побудувати таблицю SLR-аналізу для граматики із завдання 2.