Методичні вказівки до виконання контрольної роботи з дисципліни “Теорія програмування”, страница 3

Варіант 7

            Завдання 1 Написати регулярний вираз для мови, яка являє собою множину ланцюжків з 0 і 1, у яких кожна пара суміжних нулів йде перед кожною парою суміжних одиниць.

Завдання 2 За регулярним виразом (b|c)^*bc методом Томпсона побудувати ε- недетермінований автомат.

 Завдання 3 Методом побудови підмножин перетворити ε- недетермінований автомат із завдання 2 у детермінований автомат. Результатом повинна бути діаграма переходів для відповідного детермінованого автомата.

Завдання 4 Подана граматика породжує мову регулярного виразу { 0*1(0|1)* }:

S –> A1B ,  A –> 0A | ε ,   B –> 0B | 1B | ε.

Записати ліве і праве породження для ланцюжка 00011.

Завдання 5  Мовою функціонального програмування описати і застосувати функцію, що обчислює об’єм кулі за відомим радіусом.  

Завдання 6  Мовою логічного програмування написати програму з такими фактами, правилами і цілями:

Факти: трикутник A  має кути – 60, 60, 60;

  трикутник  B  має кути – 45, 45, 90.

Правило: трикутникє прямокутним, якщо один з його кутів дорівнює 90 градусам.

Ціль: чи є трикутники  A  і B  прямокутними ?

Завдання 7 Написати найслабкішу передумову для послідовності операторів

y := x + 9;

                        x := y + 8,

якщо постумовою Q останнього оператора є { x < 1 }.

Варіант 8

            Завдання 1 Написати регулярний вираз для мови, яка являє собою множину ланцюжків з 0 і 1, у яких кожна пара суміжних одиниць йде перед кожною парою суміжних нулів.

Завдання 2 За регулярним виразом (b|c)^*bcc методом Томпсона побудувати ε- недетермінований автомат.

Завдання 3 Методом побудови підмножин перетворити ε- недетермінований автомат із завдання 2 у детермінований автомат. Результатом повинна бути діаграма переходів для відповідного детермінованого автомата.

Завдання 4 Подана граматика породжує мову регулярного виразу { 0*1(0|1)* }:

S –> A1B ,  A –> 0A| ε ,   B –> 0B|1B| ε.

Записати ліве і праве породження для ланцюжка 00010.

Завдання 5 Мовою функціонального програмування описати і застосувати функцію, що обчислює відстань від довільної точки на площині до точки з координатами (2,3).

Завдання 6  Мовою логічного програмування написати програму з такими фактами, правилами і цілями:

Факти: трикутник A  має кути – 60, 60, 60;

  трикутник  B  має кути – 45, 45, 90.

Правило: трикутникє рівностороннім, якщо всі кути рівні.

Ціль: чи є трикутники  A  і B  рівносторонніми ?

Завдання 7 Написати найслабкішу передумову для послідовності операторів

y := x – 2;

                        x :=4*y + 3,

якщо постумовою Q останнього оператора є { x > 5 }.

3 ПРИКЛАДИ ВИКОНАННЯ ЗАВДАНЬ

Завдання 1 Написати регулярний вираз для мови, яка являє собою множину ланцюжків у алфавіті {a,b,c}, що містять хоча б один символ a і хоча б один символ b.

Клас регулярних виразів визначається такими правилами:

1     є регулярним виразом.

2    Якщо а А, то а – регулярний вираз.

3  Якщо w – регулярний вираз, то w^* і (w) – регулярні вирази.

4   Якщо w₁ і w₂ – регулярні вирази, то w₁w₂, w₁|w₂  – регулярні вирази. У виразі w₁w₂ використовується операція конкатенації, у виразі w₁|w₂ – операція об'єднання.  

Потрібний вираз може бути представлений, наприклад, у такій формі:

   ( (a|b|c)a(a||b|c)b(a|b|c) ) | ( (a|b|c)b(a||b|c)a(a|b|c) ) .

Завдання 2 За регулярним виразом (a|b)^*a методом Томпсона побудувати ε- недетермінований автомат.

            Розбираємо регулярний вираз r на складові підвирази. Для кожного базового символу з r, що є або символом алфавіту, або , будуємо базові недетерміновані автомати.

Потім відповідно до структури r комбінуємо базові недетерміновані автомати, поки не одержимо автомат для усього виразу.

            Позначимо недетермінований автомат для s через N(s), а недетермінований автомат для t через N(t).

            Тоді правила комбінування можна зобразити так:

а) для s|t

ε

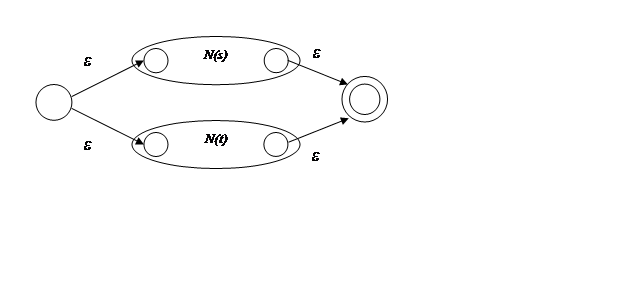
б) для st

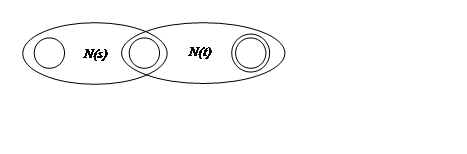
в) для s*

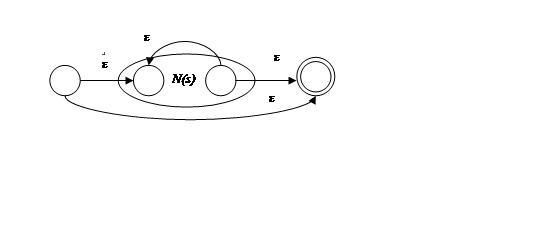
Комбінуючи дані елементи, одержимо схему для виразу (a|b)^*a.

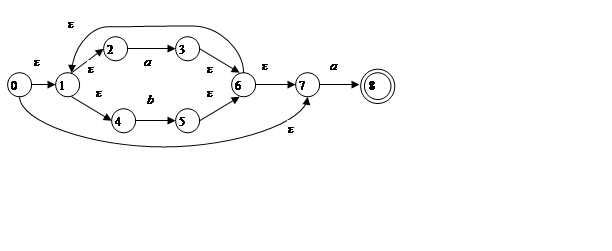
Завдання 3 Методом побудови підмножин перетворити ε- недетермінований автомат із завдання 2 у детермінований автомат. Результатом повинна бути діаграма переходів для відповідного ДКА.

Метод побудови підмножин полягає в наступному.

Спочатку будується ε-замикання для вихідного стану 0. У замикання входять усі стани, що досяжні з вихідного по переходах . Для даної схеми

-close{0}= {0,1,2,4,7},

З підмножини A по символу a можна перейти до підмножини {3,8}. Замиканням підмножини {3,8} буде підмножина {1,2,3,4,6,7,8}, яку  позначимо буквою B.