Метод Хука-Дживса. Исследующий поиск. Минимизация при ограничениях типа равенств. Функция Логранджа. Теорема Куна-Таккера о Седловой точке. Симплекс метод решения ЗЛП. Выбор допустимого базисного решения

24. Метод Хука-Дживса. Исследующий поиск.

   

1. Проведение исследующего поиска.  - шаг

Ищем  в котором функция уменьшается.    

2. Определим направление спуска

3. Осуществим спуск по вектору p. Переходим к 

4. Проверяем условие достижения минимума. Можно произвести редукцию . . 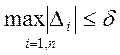Лучшая сходимость чем по симплексу.

27. Минимизация при ограничениях типа равенств. Функция Логранджа.

Пусть область U задается равенствами

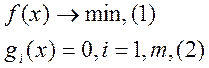Будем считать что f(x),g(x) дифер. в n-мерном пространстве и Якобиан для g(x) имеет ранг m.

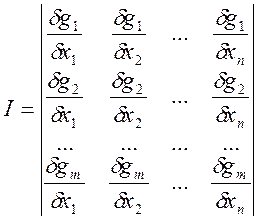
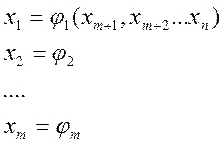   Подставим найденые переменные в ф-цию цели поелчим задачу минимизации ф-ции.В общем случае решить задачу для m неизвестных трудно решить.

Метод множетелей Логранджа.

Для решения (1) и (2) строят ф-цию: 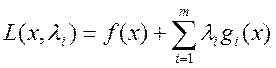, где -множетель Логранджа, которые будут  при . Тогда минимизация эквивалентна миним. (1) при условии (2). Необходимое условие минимума  .

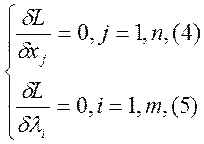
Решая эту систему получаем точки стационарности ф-и Логранджа.

Теорема. Пусть f(x) и g(x) – диферен. в  . Тогда если точка x* является решением этой задачи и Якобиан не равен 0, то сушествует  вектор , такой что 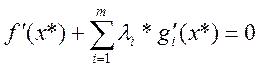 причем

29. Теорема Куна-Таккера о Седловой точке.

Теорема Куна-Такера о Седловой точке L(x)

Если т. () – седловая т. ф-и Лагранжа, удовлетворяющая условию (В), то точка х* есть точкой наименьшего значения ф-и Лагранжа для всех .

Доказательство:

Возьмем произвольное L(x,). Если < , , то значении ф-и Лагранжа будет

L(x,)f(x) в силу (8), и

Тогда:

L(x,0) =f(x). Тогда для Седловой точки получим: L(x*,0) f(x*), или просто равно.

Перепишем в виде:

f(x*)= L(x*,0)  L(x*,*) L(x,*) f(x).

Тоесть для Седловой точки ф-и Лагранжа значение ф-и цели есть минимум.

Следствие: что бы найти минимум ф-и цели достаточно найти седловую точку ф-и Лагранжа (8).

30.Общая постановка ЗЛП. Математическая модель.Формы записи ЗЛП.

В общем виде задача линейного программирования (в дальнейшем ЗЛП) может быть сформулирована как задача нахождения экстремального значения линейной функции 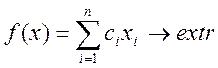 (1). на некотором множестве , где   удовлетворяют системе ограничений

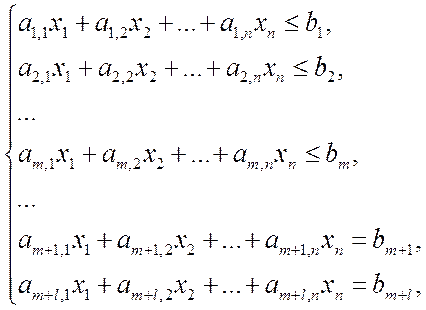и, возможно, ограничениям

.  (3)    

(2)                      

Условия (3) называют условиями неотрицательности (или тривиальными ограничениями).   

Часто условия задачи (1) - (3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращенной матричной форме    где с и х — векторы из пространства , b — вектор из пространства , a А — матрица размерности .

Задачу линейного программирования, записанную в форме (1) – (3), называют общей задачей линейного программирования.

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные , наложены условия неотрицательности, то она называется задачей линейного программирования в стандартной форме.

Задачи Л.П. – особый класс задач выпуклого кодинга.

32.Геометрическое решение ЗЛП.

Имея ЗЛП в каноническом виде, можно выбрать две произвольные переменные и, используя систему уравнений, выразить через них остальные переменные , (*) где — линейные функции. Подставив выражения (*) в целевую функцию, мы получим эквивалентную задачу  при ограничениях . Последняя ЗЛП может быть решена на плоскости.

Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки ОДР D, через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору ) до тех пор, пока не достигнем такой точки области допустимых планов D, из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с).

33.Симплекс метод решения ЗЛП. Выбор допустимого базисного решения.

Стандартной формой записи задачи Л.П. в случае «на максимум» есть

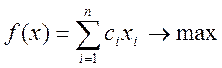
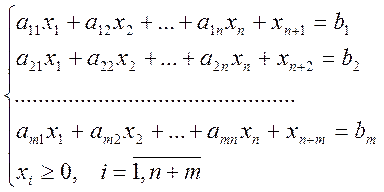
Тут  - выравнивающие переменные

Имеем систему . Можно преобразовать систему ограничений к виду:

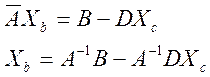
Базисное решение СЛАУ – когда свободные переменные равны 0.

При решением перебором количество решений

Решений нет, если ОДР пуста или неограниченна. ОДР для З.Л.П. – выпуклый многогранник.

35.Вырожденное решение ЗЛП.

Легко заметить, что проблемы со сходимостью симплекс-метода потенциально могут возникнуть на этапе выбора номера выводимого из базиса элемента в случае, когда одинаковые минимальные значения отношения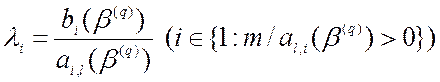

будут достигнуты для нескольких строк симплекс-таблицы одновременно. Тогда на следующей итерации столбец будет содержать нулевые элементы. Напомним, что допустимый базисный план, соответствующий базису  называется вырожденным, если некоторые его базисные компоненты равны нулю, т. е. вектор содержит нулевые элементы.

Задача ЛП, имеющая вырожденные планы, называется вырожденной. При «выходе» на вырожденный план мы лишаемся возможности корректно определить, ввод какого столбца в базис приведет к росту значения целевой функции. Подобные ситуации, в конечном счете, могут привести к зацикливанию вычислительного процесса, т. е. бесконечному перебору одних и тех же базисов.