Информатика и выч. техника \ Основы теории защиты информации

Проблемні питання сучасної асиметричної криптографії та можливі шляхи їх вирішення, страница 6

Далее, пусть существует конечное поле , где - степень простого числа. Пусть будет расширением поля и пусть существует простое число такое, что . Натуральное число существует всегда, так как и взаимно просты и, положив , получим по теореме Ферма, что . Расширенное поле по теореме Лагранжа при имеет мультипликативную подгруппу. Такая мультипликативная подгруппа содержит все элементы порядка из мультипликативной группы и единичный элемент. Так как простое число, то существует элемент порядка , и - мультипликативная подгруппа поля , которая содержит точно элементов. Обозначим эту подгруппу .

Так как и имеют одинаковый порядок , значит, они изоморфны. То есть существует отображение , которое для всех из удовлетворяет условию . Данное отображение из в строится следующим образом

.(1)

Заметим, что в общем случае группа точек на эллиптической кривой нециклическая. Поэтому при простом делителе порядка группа содержит больше, чем одну подгруппу порядка , подобную . С другой стороны, известно, что мультипликативная группа поля - циклическая. Следовательно, единственная подгруппа порядка [9]. Поэтому, используя подгруппу можно построить несколько отображений из в .

Пусть – эллиптическая кривая над конечным полем и пусть – простой делитель , такой что . Тогда существует конечное поле , которое есть наименьшим расширением конечного поля такое, что как , так и содержат элементы порядка . Набор точек с порядками кратными обычно обозначается и называется набором точек -кручения.

Мы уже знаем, что содержит как минимум разных точек -кручения [6].

Определение. Искажающим отображением точки называется эндоморфное отображение, которое переводит данную точку в линейно-независимую.

Данное отображение, переводит точку в при условии, что и имеют одинаковый порядок и либо , либо . Так как , то по определению . Предположим, что такое отображение существует. Поскольку содержит различных точек -кручения и по крайней мере одну точку-кручения, линейно независимую от других точек, следовательно . При простом , любой образующий элемент в может образовать различных точек в , следовательно, существуют точки такие, что для всех целых чисел и для всех целых чисел . Тогда содержит как минимум две такие линейно независимые точки и порядка , которые порождают векторное пространство

Это векторное пространство содержит точек, принадлежащих , так как является аддитивной группой. Таким образом, мы установили тот факт, что содержит минимум различных точек. В действительности же, содержит ровно точек, но мы не будем использовать этот последний факт.

12.5 Визначення спарювання Вейля.

Пусть будет эллиптической кривой над конечным полем , а поле будет расширением поля . Пусть будет простым числом, взаимно простым с характеристикой поля . Введем обозначение, как в работе [2], .

Спаривание Вейля – это отображение следующего вида: , где - группа корней -ой степени из единицы, являющейся подгруппой поля [9].

Допустим, что заданы две точки - кручения P и Q из множества . Из [2] известно, что можно построить две функции и , такие что

где , а . Для произвольной точки мы можем выбрать . Аналогично, для произвольной точки , можно выбрать , что не повлияет на конечный результат. Потребуем, чтобы и , а также и соответственно, не имели общих точек на , что позволит корректно определить функцию от дивизора, как 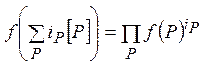[6].

Итак, зададим спаривание Вейля [8] следующим образом:

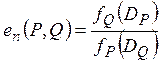Заметим, что нельзя использовать одновременно дивизоры и для получения функций и , поскольку они имеют общую точку . То есть, как минимум одна из функций должна быть построена с использованием дивизора Миллера.