На
другому кроці для кожного ![]() один раз
виконується алгоритм знаходження НСД цілих чисел. Двійкова складність алгоритму
знаходження НСД двох
один раз
виконується алгоритм знаходження НСД цілих чисел. Двійкова складність алгоритму
знаходження НСД двох ![]() -розрядних чисел дорівнює
-розрядних чисел дорівнює ![]() Тому
складність другого етапу рівна
Тому
складність другого етапу рівна ![]()
На
третьому етапі виконується не більше ![]() операцій ділення
операцій ділення ![]() -розрядного
числа на
-розрядного
числа на ![]() -розрядне
число. Тому складність цього етапу рівна
-розрядне
число. Тому складність цього етапу рівна ![]() Теорема
доведена.
Теорема
доведена.
Для факторізациі числа ![]() слід припустити
слід припустити
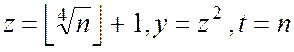 ,
звідки витікає, що складність знаходження найменшого простого дільника числа
,
звідки витікає, що складність знаходження найменшого простого дільника числа ![]() даним алгоритмом
рівна
даним алгоритмом
рівна ![]() двійкових
операцій. Якщо припустити
двійкових
операцій. Якщо припустити 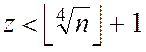 , то алгоритм шукатиме
тільки маленькі прості дільники числа
, то алгоритм шукатиме
тільки маленькі прості дільники числа ![]() .
.
Помітимо, що сучасні методи факторизації на практиці часто виконуються в 3 етапи.
Етап 1. Пробні ділення на 1¸2 тисячі перших простих чисел.
Етап 2. Знаходження
маленьких простих дільників методом Полларда або Полларда - Штрассена ( у якому
число ![]() підбирають з
міркувань оптимізації загальної трудомісткості алгоритму).
підбирають з
міркувань оптимізації загальної трудомісткості алгоритму).
Етап 3. Для знаходження великих простих дільників застосовується один з субекспоненційних алгоритмів.
![]() метод факторизації Полларда.
метод факторизації Полларда.
Припустимо, що ![]() - непарне складене число, що не має
невеликих простих дільників. Позначимо через
- непарне складене число, що не має
невеликих простих дільників. Позначимо через ![]() найменший простий дільник числа
найменший простий дільник числа ![]() . Наше
завдання полягає в його знаходженні. Припустимо, що число
. Наше
завдання полягає в його знаходженні. Припустимо, що число ![]() розкладається в добуток невеликих простих
дільників. Виберемо число
розкладається в добуток невеликих простих
дільників. Виберемо число ![]() , яке є параметром методу. Для
успішної роботи алгоритму потрібне, щоб виконувалася умова
, яке є параметром методу. Для
успішної роботи алгоритму потрібне, щоб виконувалася умова
![]()
де ![]() НСК(1,2...,
НСК(1,2...,![]() ) ( замість
) ( замість ![]() можна
використовувати
можна
використовувати ![]() або
добуток
або
добуток ![]() перших
перших
![]() простих чисел в деяких ступінях
простих чисел в деяких ступінях ![]() , які
вибираються з евристичних міркувань).
, які
вибираються з евристичних міркувань).
Через малу теорему Ферма виконується порівняння
![]()
Якщо при цьому
![]() ,
,
то
![]()
де ![]() Таким
чином,
Таким
чином, ![]() - є
власним дільником числа
- є
власним дільником числа ![]() кратним
кратним ![]()
На
цій ідеї заснований наступний метод знаходження власного дільника числа ![]() . Оскільки число
. Оскільки число ![]() невідомо,
то в ньому використаний послідовний перебір малих значень до деякого
фіксованого значення.
невідомо,
то в ньому використаний послідовний перебір малих значень до деякого
фіксованого значення.
Хай ![]() ціле число, наприклад
ціле число, наприклад ![]() і
і ![]() невелике
ціле з умовою
невелике
ціле з умовою ![]() наприклад
наприклад
![]()
Крок
1.
Для кожного ![]() від
1 до
від
1 до ![]() обчислюється
обчислюється
![]() і
перевіряємо тест кроку 2.
і
перевіряємо тест кроку 2.
Крок 2. Обчислити ![]() Якщо
Якщо ![]() , то
знайдений нетривіальний дільник числа
, то
знайдений нетривіальний дільник числа ![]() . Інакше вважаємо
. Інакше вважаємо ![]()
Наприклад.
Методом Полларда факторізовать число 247.
Хай ![]()
Обчислюємо для кожного ![]() від 1 до
від 1 до ![]()
![]() .
.
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
т.я. ![]() НСД(235-1,247)=13.
НСД(235-1,247)=13.
Нетривіальний дільник знайдений.
![]()
Можна
модифікувати алгоритм, використовуючи одночасно декілька різних основ ![]()
Оскільки
![]() , то
, то ![]() Тому як
тільки
Тому як
тільки ![]() то
то ![]() тобто
тобто![]() , і на кроці
2 буде знайдений нетривіальний дільник
, і на кроці
2 буде знайдений нетривіальний дільник ![]() .
.
Параметр ![]() повинен вибиратися не дуже великим,
інакше може бути виконано умову
повинен вибиратися не дуже великим,
інакше може бути виконано умову ![]() і дільник не буде знайдений.
і дільник не буде знайдений.
При
виконанні алгоритму зведення в ступінь ![]() треба здійснювати в кільці
треба здійснювати в кільці ![]() методом
повторного зведення в квадрат. Оскільки
методом
повторного зведення в квадрат. Оскільки![]() , то для обчислення
, то для обчислення ![]() потрібно
потрібно ![]() арифметичних
операцій кільця
арифметичних
операцій кільця ![]() .
Тому загальна складність алгоритму може бути грубо оцінена величиною
.
Тому загальна складність алгоритму може бути грубо оцінена величиною ![]()
Завдання.
Методом Полларда і ![]() -1 Полларда
факторізовать числа, вказані в таблиці 1. Оцінити складність обчислень. Варіант
брати залежно від номера в журналі.
-1 Полларда
факторізовать числа, вказані в таблиці 1. Оцінити складність обчислень. Варіант
брати залежно від номера в журналі.
|
Варіант (номер в журналі) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Число (факторизувати методом Полларда) |
143 |
187 |
221 |
247 |
253 |
347 |
323 |
437 |
391 |
77 |
249 |
377 |
|
Число(факторизувати
методом |
437 |
323 |
347 |
253 |
247 |
221 |
187 |
143 |
77 |
527 |
403 |
161 |
|
Варіант (номер в журнале) |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
Число (факторизвати методом Полларда) |
203 |
133 |
403 |
527 |
203 |
217 |
377 |
391 |
221 |
347 |
249 |
247 |
|
Число(факторизувати
методом |
341 |
403 |
249 |
377 |
143 |
299 |
217 |
77 |
527 |
187 |
323 |
341 |
Таблиця 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.