Модель систем автентифікації, страница 4

У кінцевому вигляді маємо рівняння

.                                    (1.182)

Нехай Р_з=0,5, тоді маємо

.

При n=2^m рівняння приймає вигляд

.                                         (1.183)

Дамо оцінку значення k, враховуючи що k достатньо велике і .

Тоді із (1.182) маємо

.

При Р_з =0,5 маємо

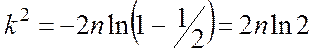
і

.                                             (1.184)

При n=2¹⁶⁰ , маємо k==2⁸⁰.

При n=2²⁵⁶, k=2¹²⁸.

При довільному значенні Р_з

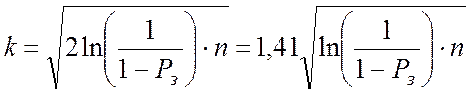.                     (1.185)

Співвідношення (1.185) дозволяє оцінити число експериментів, які необхідно виконати для здійснення колізії типу (1.176).

1.11.2 Задачі для самостійного розв’язання

1. Оцініть імовірність обману в режимі виробки та використання для забезпечення цілісності та справжності кодів автентифікації повідомлень (КАП) з довжиною L_КАП = 14, 32, 64, 128, 192 та 256 бітів. Визначте, які криптоалгоритми для автентифікації з вказаною довжиною можна застосувати.

2. Визначіть мінімальне значення k, при якому ймовірність того, що по крайній мірі у двох осіб із групи в k осіб дні народження співпадуть з ймовірністю Р_з=0,5+0,01×r , де r – номер за журналом реєстрації.

3. Визначте скільки випадкових повідомлень необхідно подати на вхід засобу розрахунку хеш-функції Н(Мі), щоб з ймовірністю Р_з=0,5+0,01×r була здійснена колізія, якщо n=2^m+k, m=192, r – номер реєстрації за журналом.

4. Розв’яжіть рівняння

,

якщо .

Визначте складність та безпечний час здійснення колізії для отриманого значення k, якщо потужність криптоаналітичної системи складає 10⁸,10¹⁰, 10¹² та 10¹⁶ опер./с., а r – номер реєстрації за журналом.

5. Дайте оцінку числа експериментів k здійснення колізій, використовуючи співвідношення (1.185)

,

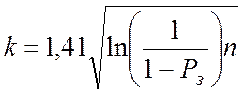якщо Р_з=0,5+0,01r, n=2^192+r, де r – номер реєстрації за журналом.

1.11.3 Контрольні запитання та завдання

1. Визначте поняття цілісності та справжності, яким чином вони забезпечуються?

2. Для чого здійснюється автентифікація повідомлень?

3. Як здійснити виробку імітовкладки з використанням симетричного криптоалгоритму?

4. Оцініть ймовірність обману в інформаційній технології, якщо для цього використовується алгоритм AES FIPS-197 з довжиною блоку 128 бітів.

5. Які основні переваги та недоліки методу автентифікації, що базується на використанні імітовкладки?

6. В чому суть парадоксу дня народження?

7. В чому суть явища виникнення колізій та як його можна реалізувати.

8. За якими показниками можна оцінити складність створення колізій?

9. Як залежить складність створення колізій від довжини хеш-функції.

10. Побудуйте графіки залежності

та

для х=0;0,1;0,2;0,3;0,4;0,5;0,6;0,7;0,8;0,9;1,0 та знайдіть значення параметра, при якому похибка складає не більше 10%.

11. Яка ймовірність того, що в групі студентів із 50 осіб двоє з них народилися в один день?

12. Яка ймовірність колізії на виході функції хешування, якщо довжина вихідного значення 128, 160, 192, 224, 256, 512 бітів і зроблено k=2¹²⁸  експериментів?

13. В чому суть парадоксу дня народження?

14. Знайдіть ймовірність перекриття гами шифруючої з періодом 2¹²⁸, якщо згенеровано відрізок 2¹⁰⁰.

15. Знайдіть довжину відрізка гами шифруючої потокового шифру при якій ймовірність перекриття не перевищує 0,6 , якщо період гами 2¹²⁸.

16. Як обчислити ймовірність колізії, якщо в (1.178) .