Джерела ключів та вимоги до них, страница 4

Із загальної теорії стійкості симетричних криптосистем випливає, що обчислювальна або безумовна стійкість шифрування забезпечується в тому випадку, якщо ключі в криптосистемі породжуються випадково, рівно ймовірно, незалежно та однорідно. Причому під ключем (ключовими даними) розумітимемо сукупність випадкових (в деяких випадках псевдовипадкових) значень змінних параметрів криптографічного перетворення інформації, за рахунок використання яких досягається мета цього перетворення. Ключові дані в симетричних криптосистемах розподіляються та розповсюджуються або з використанням спеціальних носіїв (ключових документів) або в автоматичному режимі з використанням слушних протоколів виробки та установлення ключів.

Для генерування випадкових послідовностей достатньо використати хоча б один випадковий процес. Найпростішим прикладом є зчитування стану детермінованого лічильника у випадкові моменти часу. Обов’язковою умовою для генерування випадкових послідовностей є багаторазове переповнення лічильника між моментами зчитування. Відомий спосіб генерування випадкових чисел, що базується на зчитуванні стану лічильника IBM РС в моменти натискання довільних клавіш.

Фізичні датчики шуму (резистори, напівпровідники та електронні прилади) можуть генерувати випадкові послідовності імпульсів різної амплітуди з широким спектром частоти. До сьогодні переважно в обчислювальних засобах застосовуються фізичні давачі шуму, робота яких ґрунтується на використанні зенерівського пробою (в режимі лавинного пробою). Наприклад, генератори шуму КГ401А при струмі 50...100 мА формують випадкові імпульси з амплітудою 0,1¸1 В та максимальною частотою до 3-х мГц.

На рис. 10.3 наведена схема генератора випадкових послідовностей з двома каналами формування випадкових бітів [32].

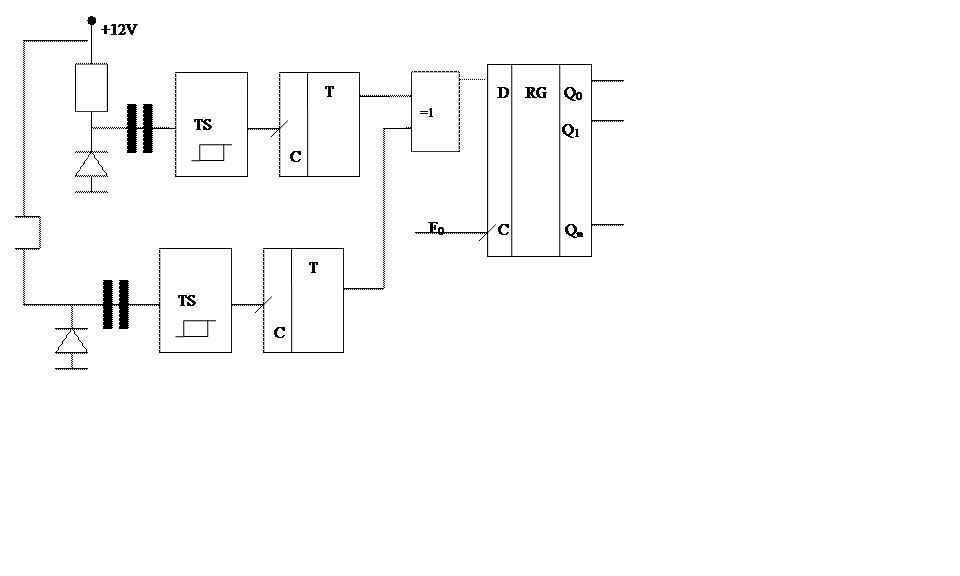
Рисунок 10.3 – Структурна схема генератора випадкових послідовностей

Можливе використання трьох і більше аналогічних каналів формування випадкових бітів.

Додаток Б

Задачі для самостійного розв’язання

Задача 1.

Визначте період повторення двійкової послідовності, що формується з використанням двох ЛРР з періодами  та , значення та  яких наведено в таблиці 2.16.

Таблиця 2.16 – Значення та

i	1	2	3	4	5	6	7	8	9	10	11	12
	13	17	19	19	89	107	127	521	89	607	31	19937
	61	13	31	17	19	13	19	89	107	127	61	9941

Задача 2.

Визначте закон формування лінійної рекурентної послідовності,  
символів  якої наведено в таблиці 2.17.

Таблиця 2.17 – Значення

і		і
1	11110001	9	111111000001
2	01001101	10	111111011010
3	11110101	11	111111001010
4	11001000	12	1110000010
5	1111100011	13	11111110000111
6	1111100110	14	00110000011011
7	1111101000	15	00000010000011
8	00100010	16	11000001010101

Задача 3.

Визначте закон формування лінійної рекурентної послідовності,  символів якої наведено в таблиці 2.18 (i=1-4), та  символів, один з яких є викривленим (і=5-8).

Таблиця 2.18

І		і
1	1110001	5	0100100000
2	1110101	6	0000101001
3	1101011	7	0110110001
4	0010001	8	0000010101

Задача 4.

Визначте обмеження на параметри та вивчіть властивості конгруентних лінійних генераторів таких видів:

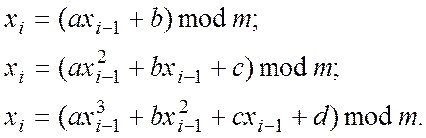
Задача 5.

Розробіть та протестуйте програму, що забезпечує формування лінійної рекурентної послідовності, якщо

Примітка. Програмно код реалізації має такий вигляд.

int LRR () {

static unsigned long shiftRegister=1;

shiftRegister = (((((shiftRegister >>7)

Ù (shiftRegister >> 5)

Ù (shiftRegister >> 3)

Ù (shiftRegister >> 1)

Ù shiftRegister))

d  0 x 00000001)

<< 31)

½(shiftRegister >> 1);

return shiftRegister d 0 x 00000001;

}.

Задача 6.

Вивчіть роботу генератора Бета-Пайпера та дослідіть його властивості [10].

Задача 7.

Вивчіть роботу, розробіть програмну реалізацію та проведіть дослідження таких генераторів рекурентних послідовностей:

–  пороговий генератор [10];

–  самопроріжуючий генератор Рюйеля [10];

–  самопроріжуючий генератор Чамберса та Голлмана [10];

–  швидкісний генератор скалярного добутку [10];

–  генератора з каскадом Голлмана [10].