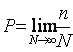Знакомство с методами измерения физических величин и методикой обработки результатов измерений, страница 2

 .                                                                  (1)

В качестве примера рассмотрим бросание игральной кости - кубика, на гранях которого нанесены цифры:  1,2,3,4,5,6. Так как в процессе бросания (испытаний) все события являются равновозможными, то вероятность выпадения какой-либо определённой (любой) цифры равна 1/6. Из определения вероятности следует, что О <Р<1, где 0-вероятность невозможного события, 1- вероятность достоверного события. Если P_i - вероятности отдельных событий, составляющих полную систему событий, то .Случайная дискретная величина считается заданной, если известны её значения и соответствующие им вероятности.

 Если случайная величина х имеет непрерывный спектр  значений, то её характеристикой является функция распределения f(x), равная по определению:   , где dP(x) — вероятность  события, что случайная величина х принимает значения в интервале . Знание функций     распределения     случайных     величин     для     обработки экспериментальных данных является крайне важным. 

Практически наиболее часто мы встречаемся с равномерным, экспоненциальным и гауссовым распределениями случайной величины.

1.3.1. Равномерное распределение случайной величины

Равномерное распределение случайной величины задается функцией:

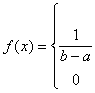
                                                       при а ≤ х ≤ b

                                            при х › b, x ‹ a