Асиметричне направлене шифрування класу RSA

Лекція № 12 а

З дисципліни  „ ОТЗІ”

Тема лекції

АСИМЕТРИЧНЕ НАПРАВЛЕНЕ ШИФРУВАННЯ КЛАСУ RSA

Навчальні питання

7.1 Алгоритми направленого шифрування

Під направленим шифруванням розуміється таке зашифровування, коли воно здійснюється на відкритому ключі одержувача, наприклад , а розшифровування здійснюється на особистому ключі . Іншими словами, направлене шифрування, коли зашифровувати можуть всі, а розшифровувати тільки один.

Повідомлення М розбивається на блоки М_і,  – розмір в бітах.

,                                                    (1.6.1)

де  – блок криптограми;

 – модуль перетворення:

                                                                (1.6.2)

де  – прості числа.

 – випадкова пара:

                                                 (1.6.3)

                                                  (1.6.4)

                     (1.6.5)

ПРОБЛЕМИ:

1. Довжини чисел  повинні бути великими:

бітів.

 повинні бути „сильними” простими числами. Число Р називається „сильним” в вузькому змісті, якщо:

,                                                       (1.6.6)

де  – просте число.

Число Р називається „сильним” в широкому змісті, якщо:

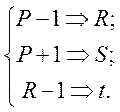                                                     (1.6.7)

де  – прості числа.

Сильні числа забезпечують максимальну крипостійкість.

В алгоритмі направленого шифрування  – є секретні параметри, а  – відкритий параметр.

2. Побудування пари ключів:

.

Пара () повинна бути випадкова, причому  повинні бути великими числами. Проблема обчислення рівняння (1.6.3).

3. Ефективність обчислень – велика складність обчислень.

7.2 Синтез ключів

Сутність проблеми:

1. Користувач повинен згенерувати  і , обчисливши рівняння (1.6.2) та (1.6.3).

2. Обчислення  із рівняння (1.6.3):

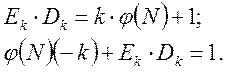                                                           (1.6.9)

Діафантове рівняння:

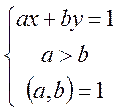                                                      (1.6.10)

де  – взаємопрості числа.

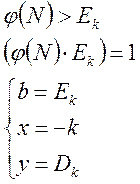
Розв’язок (1.6.10):

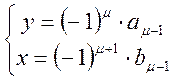,                                           (1.6.11)

де  – параметри ланцюгового дробу виду :

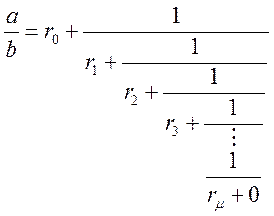                                       (1.6.12)

 – останній лишок, у якого лишок = 0.

Розглянемо

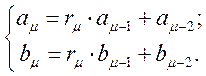                                                   (1.6.13)

Підставивши (1.6.13) в (1.6.11) одержуємо розв’язок, визначаємо невідомі . Таким чином, визначаємо . Для перевірки розв’язку підставляємо значення в (1.6.3).

Проблемні питання:

1.  Великі числа. Треба використовувати багатослівну арифметику.

2.  Розв’язок задачі, тобто  є випадковою. Залежить від розміру . Дуже важливо знати середню величину :

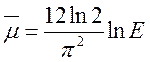,                                             (1.6.14)

де Е – величина ключів.

7.3 Оцінка крипостійкості

В RSA криптосистемі можна виділити:

Відкриті параметри:

Конфіденційні параметри:

Криптоаналітик повинен знайти . Для цього:

1)  криптоаналітик перехоплює  і ;

2)  криптоаналітик повинен факторизувати ;

3)  криптоаналітик обчислює функцію Ейлера: ;

4)  криптоаналітик обчислює .

Задача факторизації є самою складною задачею криптоаналізу.

Висновок:

RSA є імовірностійкою криптосистемою і сутність криптоаналізу зводиться до факторизації  на два прості числа:  та . Складність криптоаналізу є субекспоненційною.

Методи:

1) метод спробного ділення:

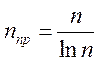                                                   (1.6.16)

;

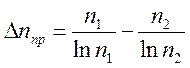2) метод -Поларда – базується на теорії колізії;

3) метод Ленстри – базується на еліптичних кривих;

4) метод „дійкове решето”.