Информатика и выч. техника \ Основы теории защиты информации

Асиметричне криптографічне RSA перетворення направленого шифрування класу RSA, страница 4

Визначення 1. Функцією гешування називається функція відображення h: D → R , де область значень D ={0,1}*, а R ={0,1}n для деякого n ≥ 1.

Визначення 2. Функцією стиску називається функція відображення f: D → R, де

D ={0,1}a × {0,1}b  і R ={0,1}n для деяких a, b, n ≥ 1 і a + b ≥ n.

Визначення 3. Ітераційною функцією гешування від функції стиску f: ({0,1}n × {0,1}b) → {0,1}n  є функція гешування h: ({0,1}b)* → {0,1}n визначена h(X1...Xt)=Ht, де Hi=f(Hi−1,Xi) при 1 ≤ i ≤ t (H0 = IV).

Більшість функцій гешуванняце ітеративні конструкції, що використовують функцію стиску f, попередня розбивка даних X на підблоки Xi та зв'язування по зворотному вході проміжних результатів обчислень геш-значень. Стандартна модель ітеративної функції гешування визначена в ISO/IEC 10118.

 На рис. 11.1 наведена загальна модель ітеративної функції гешування.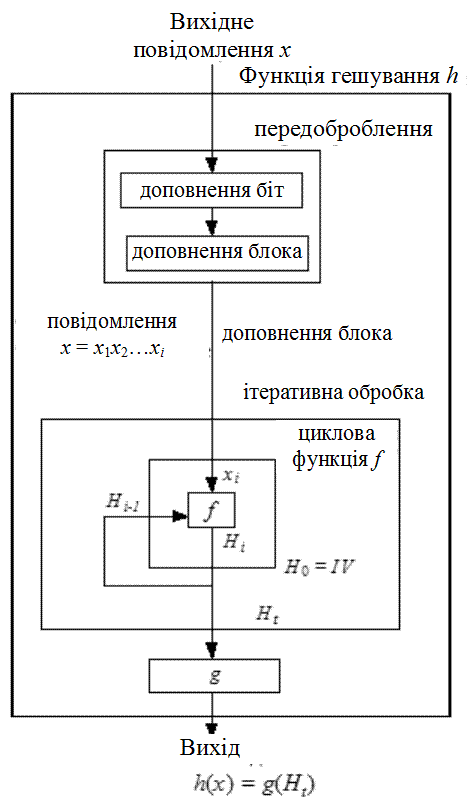

Рисунок 11.1– Ітеративна модель функції гешування

Узагальнена модель ітеративної функції гешування для t підблоків визначається наступним алгоритмом ітеративних обчислень

H0 = IV

Hi = f(Hi-1,Xi) , 1≤ i ≤t,                                         (6.1)

h(K,X) = g(Ht) .

Тут IV позначає початкове значення, що може бути визначене як деяка константа в описі функції гешування і g є вихідним результуючим перетворенням.

Стандарт ISO/IEC 10118 не визначає методи доповнення рядка даних, але передбачається, що можуть бути використані методи, визначені в ISO/IEC 9797.

Визначальними вимогами до функцій гешування є їх стійкість до обчислення прообразу, другого прообразу, а також стійкість до колізій [145].

Визначення 4 (Стійкість до обчислення прообразу) [149]. Функція гешування h:{0,1}* → R є стійкою до обчислення прообразу (t,є), якщо не існує імовірнісного алгоритму Ih, із вхідними значеннями YÎ R і значеннями на виході XÎ{0,1}*, часом виконання не більш ніж t, де h(X)=Y і імовірністю не менше, чим оцінена при випадковому виборі Y і Ih.

Стійкість функції гешування до обчислення прообразу визначає її як однобічну в тому змісті, що при даному значенні функції гешування практично неможливо визначити повідомлення для якого воно було обчислено. Ця властивість функції гешування має важливе значення для систем автентифікації, що використовують геш-значення паролів і таємних ключів.

Визначення 5 (Стійкість до обчислення другого прообразу) [149]. Нехай S – кінцева підмножина {0,1}*. Функція гешування h:{0,1}*→ R є стійкою до обчислення другого прообразу з захищеністю (t,є,S), якщо не існує імовірнісного  алгоритму Sh, з XÎr S і X'Î{0,1}*, часом виконання не більш ніж t, де X' ≠ X і h(X') = h(X) і імовірністю не менш є, що оцінена при випадковому виборі X і Sh.

Стійкість функцій гешування до обчислення другого прообразу визначає безпеку систем автентифікації.

Визначення 6 (Стійкість до колізій) [183]. Функція гешування h: {0,1}* → R є стійкою до колізій захищеністю (t, є), якщо не існує імовірнісного алгоритму Ch з відомими вихідними значеннями X,X'Î{0,1}*, часом виконання не більш ніж t, де X'≠X і h(X)=h(X') і  імовірністю не менш є, що оцінена при випадковому виборі Ch.

Стійкість функцій гешування до колізій визначає безпеку систем автентифікації з цифровим підписом.

Визначення 7. Функція гешування називається простою або слабкою(однонаправленою) [174], якщо є стійкою до обчислення прообразу і стійкою до обчислення другого прообразу.

Визначення 8. Функція гешування називається сильною або колізійностійкою [174], якщо є стійкою до обчислення прообразу, стійкою до обчислення другого прообразу і стійкою до колізій.

Визначення сильної функції гешування показує, що обчислювано неможливо знайти яку-небудь колізію і захищає проти класу атак, відомих як атака «день народження» [171].

Всі атаки на функції гешування можна розділити на дві групи: атаки, засновані на уразливості алгоритму перетворень (аналітичні) і атаки, що не залежать від алгоритму.

Однобічні і колізійно-стійкі функції гешування не використовують при обчисленнях секретну інформацію. Отже, немає необхідності класифікувати атаки в залежності від таких характеристик інформації і їх доступності порушником. Ціль порушника полягає в знаходженні першого або другого прообразу для геш-значень, або за допомогою колізії нав'язування помилкових даних. Забезпечення стійкості до колізії необхідно в схемах цифрового підпису, де використовуються однобічні функцій гешування. Слід зазначити, що деякі атаки засновані на визначенні прообразу або колізії для випадкових повідомлень, інші надають порушнику досить свободи у виборі необхідних текстів даних.

Скачать файл