Удаление одной вершины так, чтобы в полученном орграфе не было циклов

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Курсовая работа

по практикуму на ЭВМ: структуры данных и алгоритмы

Факультет               прикладной математики и информатики          

Группа                    ПМ-71

Студент                  Новикова Т.С.

Преподаватель    Еланцева И.Л.

Новосибирск  2008

1.  Условие задачи.

Задан орграф с циклами. Проверить, можно ли удалить одну вершину так, чтобы в полученном орграфе не было циклов.

2. Анализ задачи.

Основные определения

Графом G(V,E) называется совокупность двух множеств, где V – конечное непустое множество элементов, называемых вершинами ,а E – множество неупорядоченных пар различных элементов множества V(эти пары называются рёбрами). 

Говорят, что ребро e=(u,v) соединяет вершины u и v. Ребро е и вершина

u(а также e и v) называются инцидентными, а вершины u и v – смежными.

Рёбра, инцидентные одной и той же вершине также называются смежными. 

Число  вершин  графа называется его  порядком.

Степенью  вершины графа называется количество  смежных  с ней вершин.

Вершина v называется достижимой из  вершины u, если существует (v,u) – маршрут.

Маршрут (путь) – это чередующаяся последовательность:

а=v0, e1, v1,  e2,…,vn 1, e n,v n=b

вершин и рёбер графа такая, что ei=(vi-1,vi), 1<=i<=n. Говорят, что маршрут соединяет вершины a и b –концы маршрута. В простом графе маршрут можно задать перечислением лишь его вершин a=v0,v 1,…,v n=b или его рёбер e1 ,e2,..,e n.

Маршрут называется цепью, если все его рёбра различные. Маршрут называется замкнутым, если  v 0=v n.

Замкнутая цепь называется циклом. Цепь называется простой, если не содержит одинаковых вершин. Простая замкнутая цепь называется простым циклом.

Ребро графа называется ориентированным, если существен порядок расположения его концов. Граф, все рёбра которого ориентированные, называется ориентированным графом (или орграфом). В этом случае элементы множества  называются узлами, а элементы множества  - дугами. Дуга () ведёт от вершины  к вершине . вершину  называют преемником вершины  , а  - предшественником вершины .

Источник орграфа – это вершина, от которой достижимы все остальные вершины. Сток орграфа – это вершина, достижимая со всех других вершин.

Дано:

Входной файл “graph.txt”.

G=(V_G ,E_G ), E={(u,v)I u,v є VG}

Найти: t є { 0,1 }

Метод решения:

Создаём матрицу смежности графа G (матрица смежности – матрица размером n x n, где строчка – одна вершина, а ячейка из этой строчки равна 1, если из этой вершины есть дуга в вершину, с номером, совпадающим с номером столбца, и равна 0 в противном случае).

Сначала все ее элементы считаем равными 0.

pi – первая вершина;

i=1,n;

n – количество вершин;

i=0;

k=pi;

i=1;

Повторять:

  если (deg(k)>=2)

удалить k;

если граф ацикличен, то вывод «можно» и j=1;

восстановить  k;

k= очередная вершина G со степенью > 1;

i=i+1;

пока i<=n.

3.Структуры данных.

Входные данные:

Внешнее представление:  

Входные данные представлены графом G. В памяти компьютера граф G представлен матрицей смежности.

Матрица A=(a_ij), i=1,2..n; j=1,2..n;

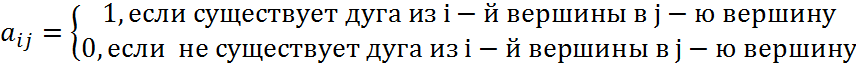
Матрица смежности в данном случае не дублирует информацию (так как граф ориентированный, то матрица не симметрична). Матрица смежности позволяет однозначно задавать граф. Преимуществом такого представления является «прямой доступ» к ребрам графа.

Внешнее представление графа, т.е. как он представлен в файле входных данных выглядит следующим образом:

n   m                   где n –количество вершин

a1  a2                        m – количество дуг

a3  a4                        [a1,a2] –дуга графа

.   .    .                

Существуют и другие методы представления графа:

Список ребер – не дублирует информацию, представляется двумя массивами. Неудобством является большое число шагов, необходимое для получения множества вершин, к которым ведут рёбра из данной вершины, а это существенный недостаток для данной задачи.

Матрица инцидентности – матрица, строки которой соответствуют вершинам, а столбцы – рёбрам, заполненные таким образом, что элемент равен 1, если вершина инцидентна ребру, 0 в противном случае. Недостаток данного представления в использовании лишней памяти, в основном занятой нулями, к тому же её формирование сложно для пользователя.

Входными данными являются  целые числа - количество вершин циклического орграфа, а также удаляемая вершина.

Внутреннее представление:

Результатом будет последовательность вершин, которые являются точками сочленения данного графа. В памяти компьютера эта последовательность представлена линейным односвязным ациклическим списком с фиктивным звеном.

Выходные данные:

Внешнее представление:

При i=0, сообщение "no", а при i=1 сообщение "yes"

Внутреннее представление:

i=0||1

4. Укрупненный алгоритм решения задачи.

 

5. Структура программы.