Сравнение скорости выполнения прямого, обратного и случайного обхода массива (Лабораторная работа № 2)

1. Характеристика системы:

Процессор AMD Athlon(tm) XP 1900+	Физическая частота	1607,5 MHz
	FSB	133 MHz
	Скорость шины процессора	266 MHz
L1 cache (Работает на частоте процессора)	КЭШ данных размер строки степень ассоциативности	64 Кб 64 байта 2
	КЭШ команд размер строки степень ассоциативности	64 Кб 64 байта  2
L2 cache (Работает на частоте процессора)	Объем Размер строки Степень ассоциативности	256 Кб 64 байта 16
Оперативная память	DDR-SDRAM PC3200	256 Мб
ОС	Microsoft  Windows 2003
Компилятор	Borland C++ Compiler v5.5

2. Задача 1

Сравнить скорость выполнения прямого, обратного и случайного обхода массива   

#include "stdafx.h"

#include<stdio.h>

#include<conio.h>

unsigned int const STEPS=10;

unsigned long clock()

{

    _asm rdtsc

}

void _tmain()

{

    unsigned long*arr;

    FILE*fpt,*fpn;

    unsigned long i;

    float size;

    unsigned long N;

    unsigned int t;

    unsigned long k;

    fpt=fopen("t.txt","w");

    fpn=fopen("n.txt","w");

    for(size=0.5,N=128;size<1024;size+=0.5,t=0)

    {

        N=size*1024/4;

        arr=new unsigned long[N];

        for(i=0;i<N;i++)

        {

            arr[i]=-1;

        }

        unsigned long pos;

        for(i=0;i<N;i++)

        {

            pos=double(rand())/RAND_MAX*(N-1);

            while(arr[pos]!=-1)

            {

                pos++;

                if(pos==N)

                {

                    pos=0;

                }

            }

            arr[pos]=i;

        }

//      for(i=0;i<N-1;i++)arr[i]=i+1;

//      arr[i]=0;

//      arr[0]=N-1;

//      for(i=1;i<N;i++)arr[i]=i-1;

//      for(i=0;i<N;i++)printf("%d\t%d\n",i,arr[i]);

        t=clock();

        for(i=0,k=0;i<STEPS*N;i++)

        {

            k=arr[k];

        }

        t=clock()-t;

        fprintf(fpn,"%f\n",size);

        fprintf(fpt,"%f\n",static_cast<double>(t)/static_cast<double>(N)/

            static_cast<double>(STEPS));///static_cast<double>(CLK_TCK));

        delete[] arr;

    }

}

Результаты работы программы можно увидеть на рис 1.

Просмотрев графики, можно убедиться, что наиболее быстрым является прямой обход. Это происходит благодаря механизмам кэширования и аппаратной предвыборки. Чуть медленнее выполняется обратный обход, потому как кэширование для него по-прежнему эффективно, в отличие от аппаратной предвыборки, которая не приносит пользы. График случайного обхода хаотичен, т.к. при случайном обращении вероятность кэш-промаха стремится к 1, а механизм аппаратной предвыборки не работает (минимальные пики на графике соответствуют операции обращения к элементу, уже положенному в кэш).

Так же на графиках прямого и обратного обходов прослеживаются ситуации выхода массива за пределы кэш-памяти первого (64Кб) и второго уровней (320Кб).

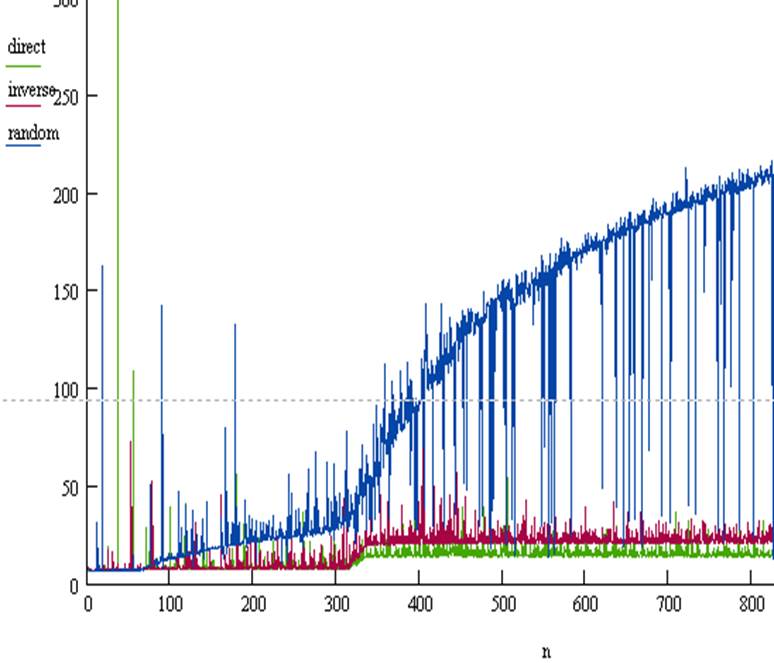
Рис 1. график зависимости скорости обхода от количества элементов в массиве

3. задача 2

Определить степень ассоциативности L1-cache.

#include<stdio.h>

#include<conio.h>

unsigned int const block_size=64*1024/4;

unsigned int const offset=1024*1024/4;

unsigned long clock()

{

    __asm rdtsc

}

void main()

{

    unsigned*arr;

    unsigned i,j,k;

    unsigned n,t;

    FILE*fp,*fp1;

    fp=fopen("t.txt","w");

    fp1=fopen("t1.txt","w");

    for(n=1;n<=20;n++)

    {

        arr=new unsigned[offset*n];

        for(i=0;i<offset*n;i++)arr[i]=1;

        for(i=0;i<n-1;i++)

        {

            for(j=0;j<block_size/n;j++)

            {

                arr[i*offset+j]=(i+1)*offset+j;

            }

        }

        for(j=0;j<block_size/n-1;j++)

        {

            arr[(n-1)*offset+j]=j+1;

        }

        arr[(n-1)*offset+j]=0;

        k=0;

        for(t=clock(),i=0;i<block_size;i++)

        {

            k=arr[k];

        }

        t=clock()-t;

        if(k==-1)return;

        fprintf(fp,"%f\n",(float)t/(float)block_size);

        fprintf(fp1,"%d\n",n);

        delete[]arr;

    }

    fclose(fp);

    fclose(fp1);

    return;

}

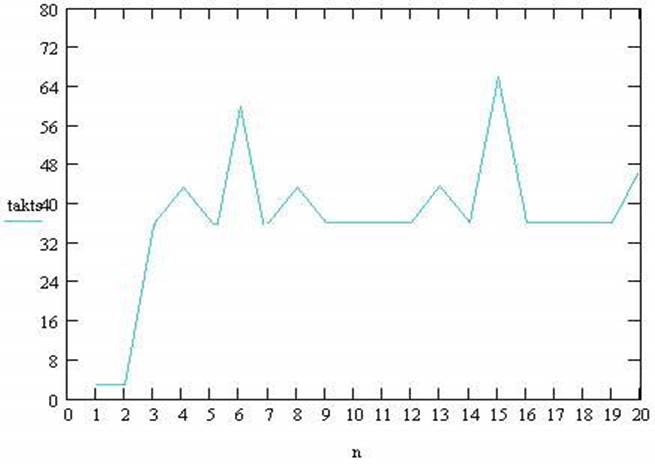
На рис2. представлен график зависимости времени обработки одного элемента массива от количества блоков. На графике наблюдается увеличение количества тактов на обработку одного элемента при изменении количества блоков с 2 до 3. Вывод: ассоциативность L1-cache равна 2, - что соответствует действительности.