№4
|
№ |
класс |
расстояние |
|
0 |
1 |
5 |
|
1 |
2 |
1 |
|
2 |
2 |
4 |
|
3 |
4 |
4 |
|
4 |
3 |
1 |
|
5 |
5 |
3 |
|
6 |
1 |
5 |
|
№ |
Принятые самолеты |
Кол-во принятых |
класс |
Макс-е кол-во |
Расстояния до самолетов |
||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|||||||||||
|
0 |
0 |
6 |
2 |
3 |
2 |
5 |
3 |
9 |
2 |
15 |
2 |
4 |
|||||
|
1 |
2 |
2 |
2 |
4 |
7 |
5 |
9 |
9 |
1 |
7 |
|||||||
|
2 |
5 |
1 |
5 |
1 |
2 |
2 |
5 |
8 |
7 |
2 |
11 |
||||||
2)
P1=do x,y: = x + y, y - 1 until y = 0 od
1)Преобразуем программу P1 в эквивалентную программу P2.
P2 = x,y : = x + y, y - 1; while y ≠ 0 do x,y := x + y, y - 1 od
Докажем, что [P1] = [P2]. Регулярное выражение, соответствующее P1, будет выражение (ab)+, если символом ‘a ‘ будем обозначать оператор x:= x + y, а символом ‘ b’ будем обозначать оператор y: = y - 1.
Регулярное выражение соответствующее P2 – ( ab) (ab)* = (ab)+.
Таким образом, программы P1 и P2 эквивалентны по выполнению и следовательно, эти программы эквивалентны функциональны. В этом случае достаточно доказать правильность программы P2.
Программа P2 не является элементарной программой. Следовательно, для доказательства её правильности необходимо выделить элементарные подпрограммы, из которых сконструирована программа P2.
P2 = x,y := x + y, y - 1; P‘2;
P‘2 = while y ≠ 0 do x,y := x + y, y - 1 od
Теперь рассмотрим подпрограмму P‘2. Определить программную функцию и инвариант для этой программы: цикл не зацикливается при
y ³ 0, так как на каждом шаге ‘y’ уменьшается на единицу, а к ‘x’ прибавляется ‘y’, таким образом, начальное значение ‘x’ увеличится на 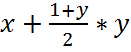 .
.
Следовательно, предполагаемая
функция f=( y³0®x, y: = 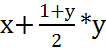 , 0) Естественно, что с начала необходимо доказать правильность
определённой функции, и только потом, используя эту функцию, строить инвариант
для данной элементарной, циклической программы.
, 0) Естественно, что с начала необходимо доказать правильность
определённой функции, и только потом, используя эту функцию, строить инвариант
для данной элементарной, циклической программы.
function (x,y - целые числа)
f=( y³0®x, y: = 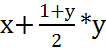 , 0)
, 0)
program
while y ≠ 0 do x,y := x + y, y - 1 od
proof
term
Начальное значение y ≥ 0 при каждой итерации уменьшается на 1, так что в итоге
while _ тест примет значение ложно
pass
while_test true ( доказать (p ® f)=(p ® f ° g))
|
фрагмент |
условие |
x |
y |
|
y ≠ 0 |
y0 ≠ 0 |
x1=x0 |
y1=y0 |
|
x,y := x + y, y - 1 |
x2 = x1 + y1 |
y2 = y1 - 1 |
|
|
f=( y³0®x, y: = |
y2 ³ 0 |
x3= |
y3= 0 |
выводы:
а) условие: y ≠ 0
условие: y0 ¹ 0L y2 ³ 0 = y0 ¹ 0L y1 - 1³ 0
= y0 ¹ 0L y0 - 1³ 0
= y0 ¹ 0L y0 ³ 1
= y0 > 0
б) присваивание: x3 = 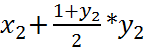
= 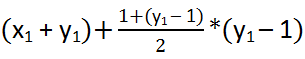
= 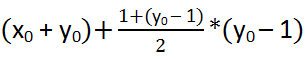
=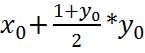
Функция программы:
f=(y > 0®x, y:=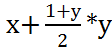 , 0), которая при значении while _теста истина совпадает с
заданной функцией.
, 0), которая при значении while _теста истина совпадает с
заданной функцией.
pass
while_test false (доказать ( Ø p ® f ) = (Øp ® I))
(y = 0 ®( y ³ 0®x, y := 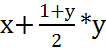 , 0))
, 0))
= (y =
0 ® x, y := 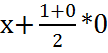 , 0)
, 0)
= (x = 0 ® x, y := x, y)
т.е. получили тождественную функцию, что и требовалось доказать
pass
result
pass comp
3) определим инвариант:
|
X |
f(X) |
f(X0) |
|
x |
|
|
|
y |
0 |
0 |
Согласно теореме об инвариантах для построения инварианта необходимо приравнять компоненты, соответствующие f(X) и f(X0):
1) 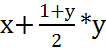 =
= ![]()
2) 0 = 0
Первый инвариант
представляет интерес, т.к. характеризует функцию. Учитывая второе соотношение
у = у0, предикат 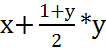 =
= 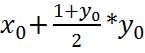 перепишем (x - x0) =
перепишем (x - x0) =![]() -
- 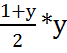 . 1) этот предикат верен перед выполнением цикла, т.к. x = x0,
а y = y0; 2) этот предикат выполняется во время
выполнения цикла (x - x0) =
. 1) этот предикат верен перед выполнением цикла, т.к. x = x0,
а y = y0; 2) этот предикат выполняется во время
выполнения цикла (x - x0) =![]() -
- 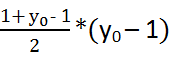 ; 3) после выполнения цикла у = 0. Следовательно, получаем (x - x0)
=
; 3) после выполнения цикла у = 0. Следовательно, получаем (x - x0)
=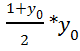 , а это есть предикат x =х0 +
, а это есть предикат x =х0 +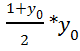 L у = 0, что соответствует функции программы.
L у = 0, что соответствует функции программы.
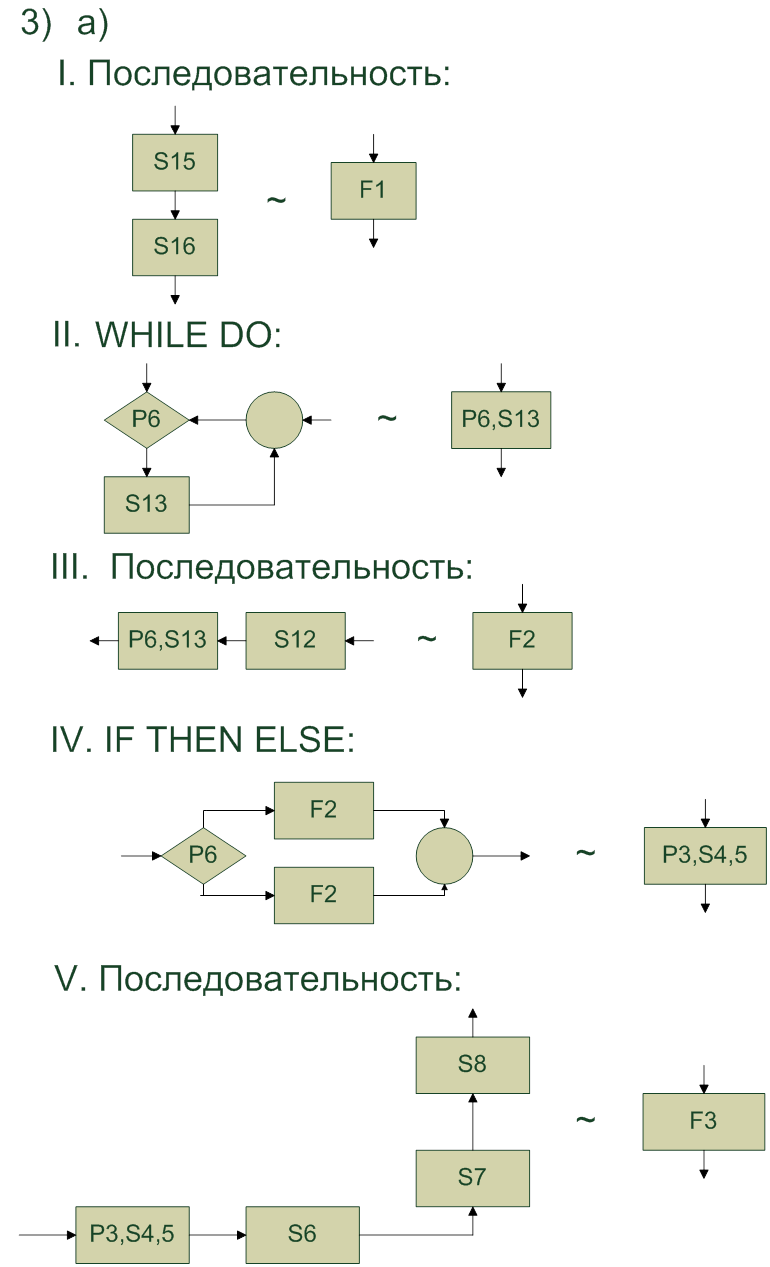
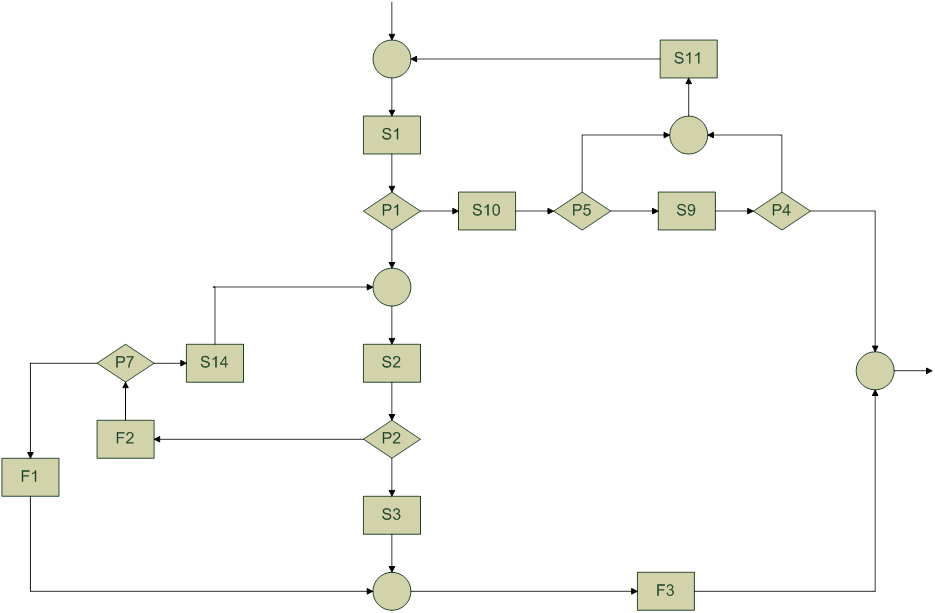
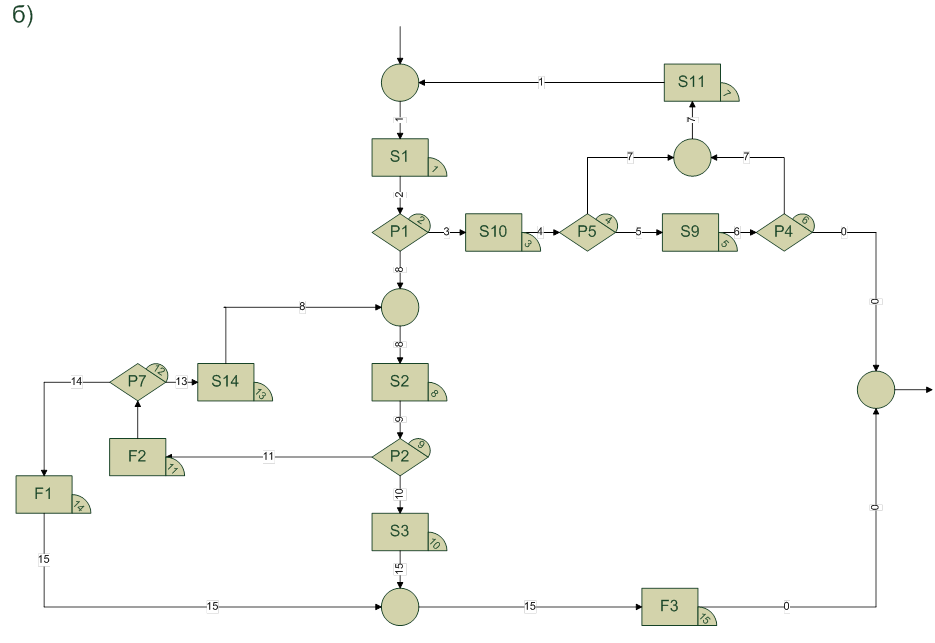
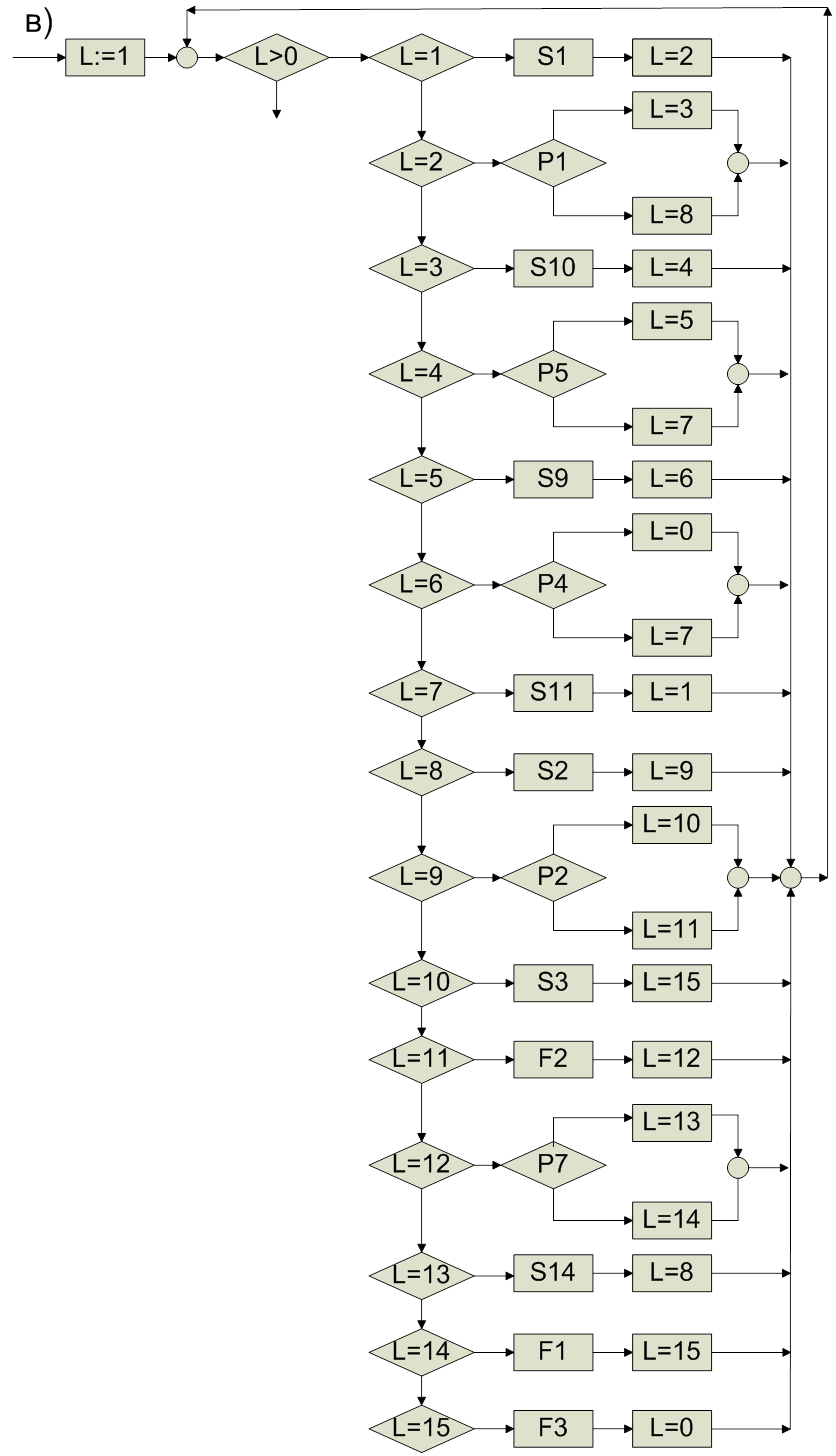
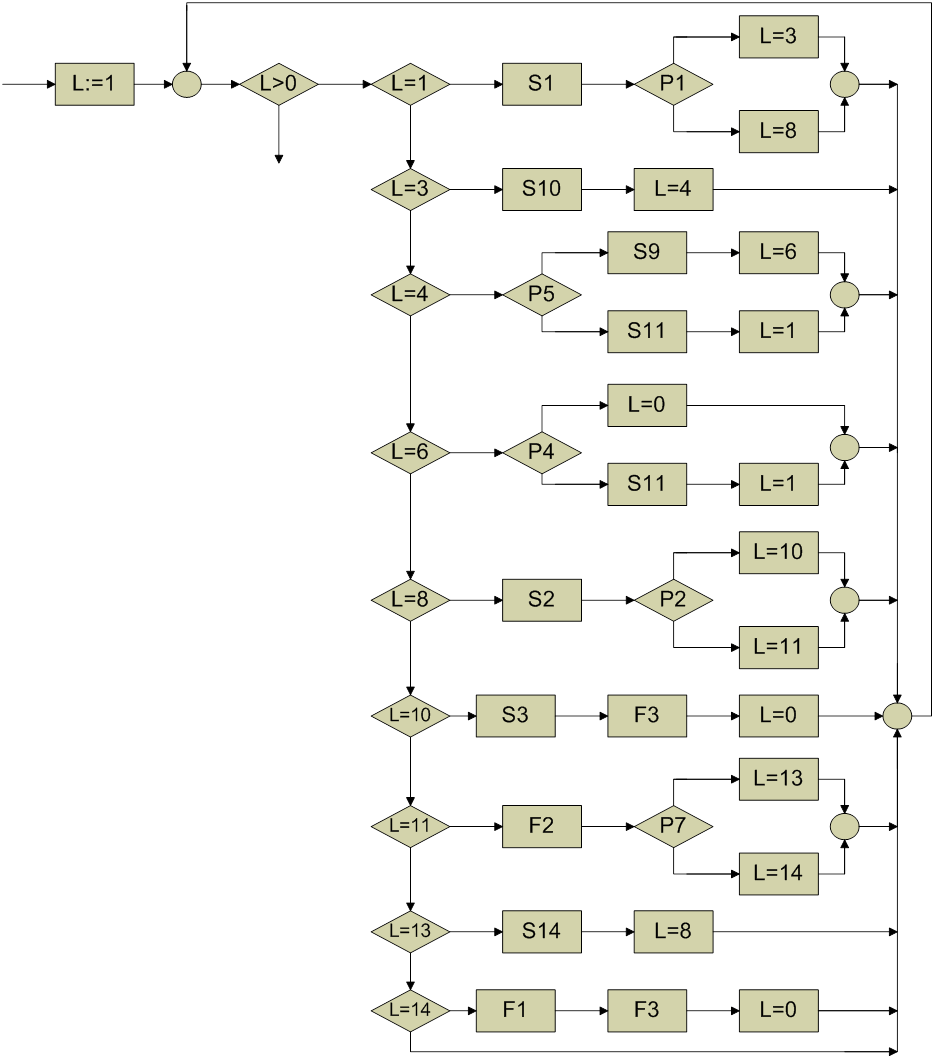
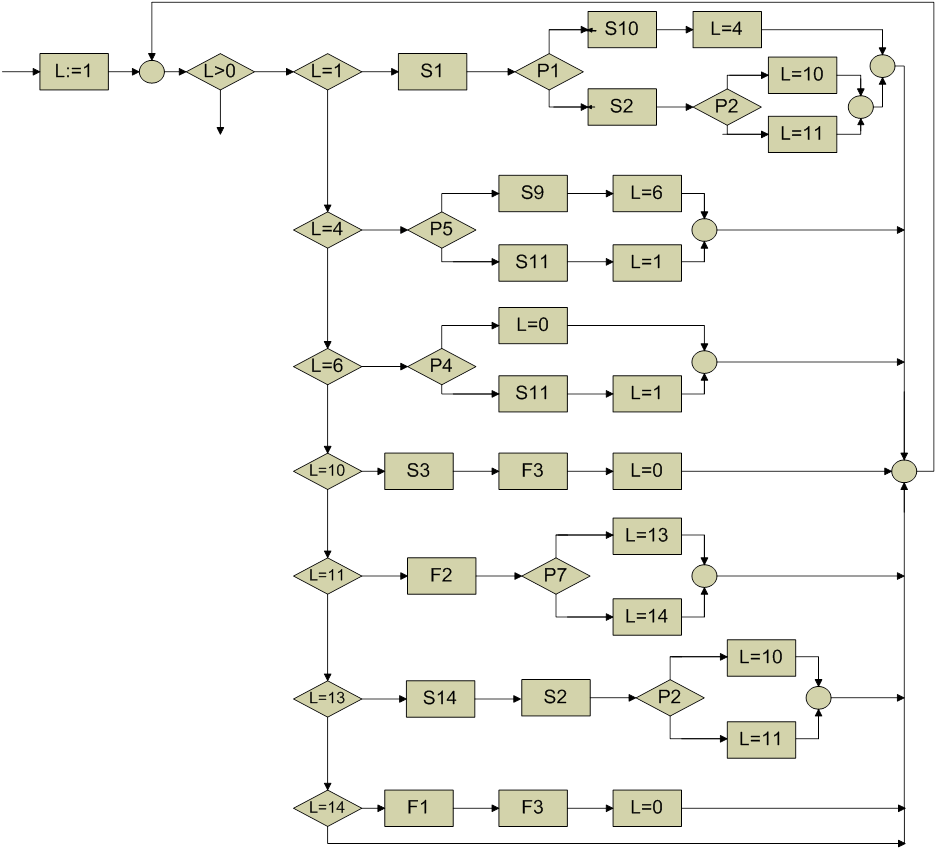
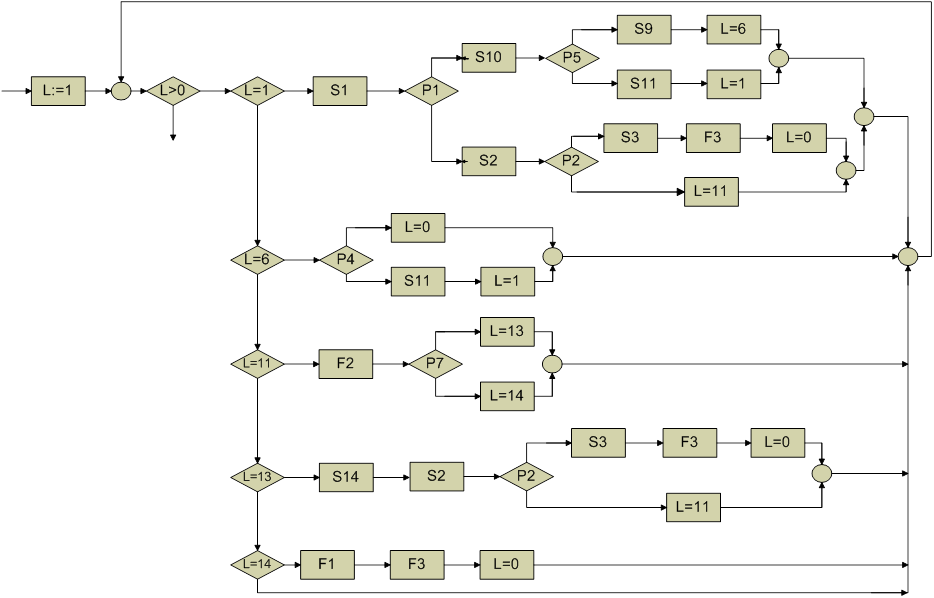
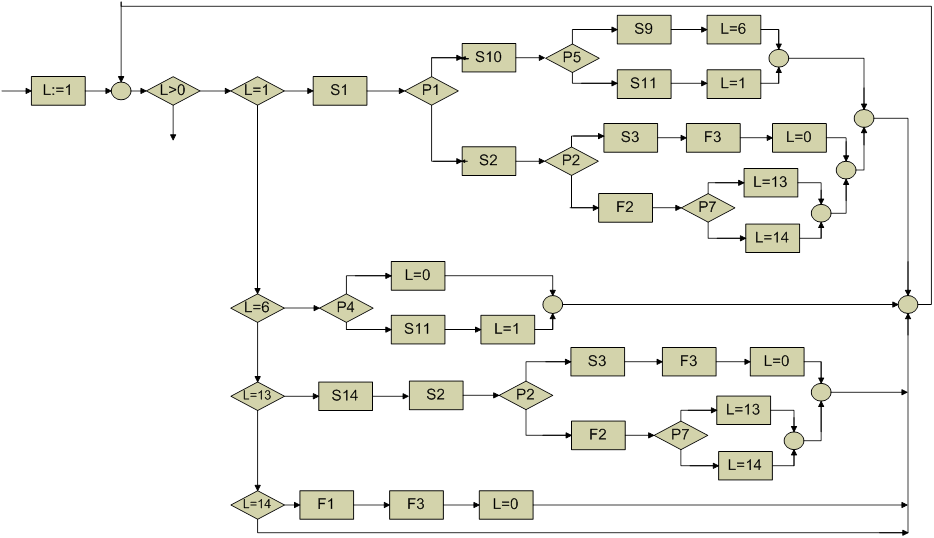
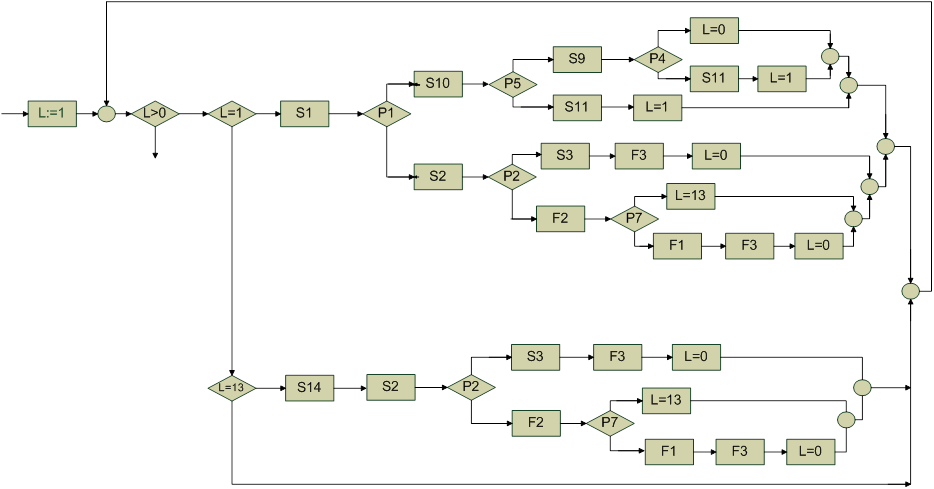
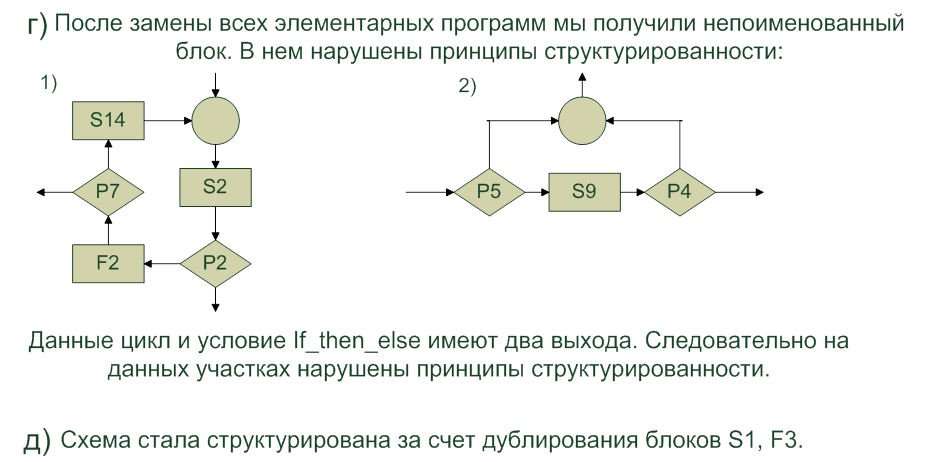
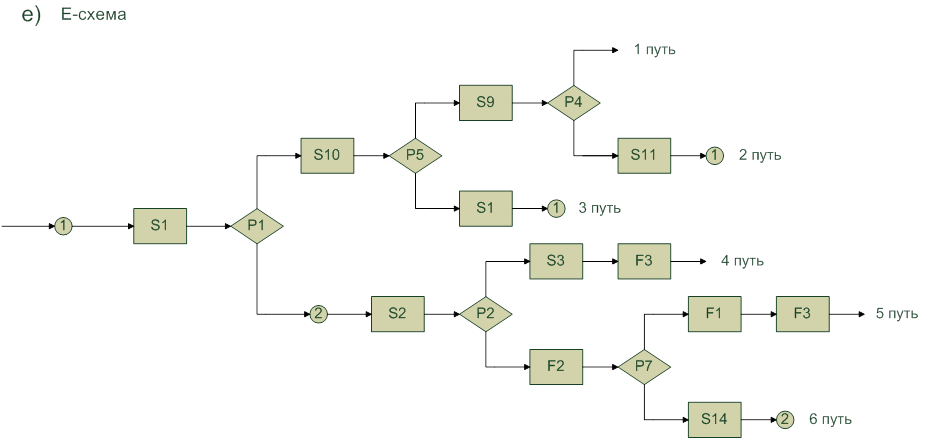
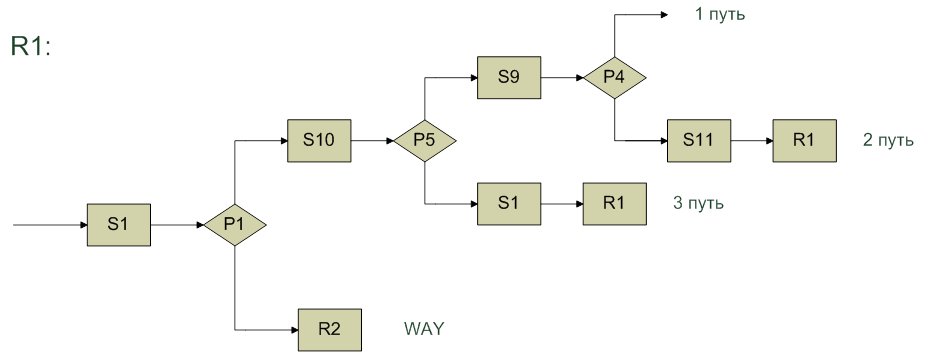
1 путь:
P1(S1(X)) ΛP5(S10(S1(X))) ΛP4(S9(S10(S1(X)))) ΛY=S9(S10(S1(X))) ;
P1![]() S1(X) ΛP5
S1(X) ΛP5![]() S10
S10![]() S1(X) ΛP4
S1(X) ΛP4![]() S9
S9![]() S10
S10![]() S1(X) →Y=S9
S1(X) →Y=S9![]() S10
S10![]() S1(X) .
S1(X) .
2 путь:
P1(S1(X))ΛP5(S10(S1(X)))Λ![]() P4(S9(S10(S1(X)))) ΛY=R1(S11(S9(S10(S1(X)))))
;
P4(S9(S10(S1(X)))) ΛY=R1(S11(S9(S10(S1(X)))))
;
P1![]() S1(X)ΛP5
S1(X)ΛP5![]() S10(X)Λ
S10(X)Λ![]() P4
P4![]() S9
S9![]() S10
S10![]() S1(X) →Y=R1
S1(X) →Y=R1![]() S11
S11![]() S9
S9![]() S10
S10![]() S1(X) .
S1(X) .
3 путь:
P1(S1(X))Λ![]() P5(S10(S1(X))) ΛY=R1(S1(S10(S1(X))))
;
P5(S10(S1(X))) ΛY=R1(S1(S10(S1(X))))
;
P1![]() S1(X)Λ
S1(X)Λ![]() P5
P5![]() S10
S10![]() S1(X) →Y=R1
S1(X) →Y=R1![]() S1
S1![]() S10
S10![]() S1(X) .
S1(X) .
WAY:
![]() P1(S1(X))ΛY=R2(S1(X));
P1(S1(X))ΛY=R2(S1(X));
![]() P1
P1![]() S1(X) →Y=R2
S1(X) →Y=R2![]() S1(X).
S1(X).
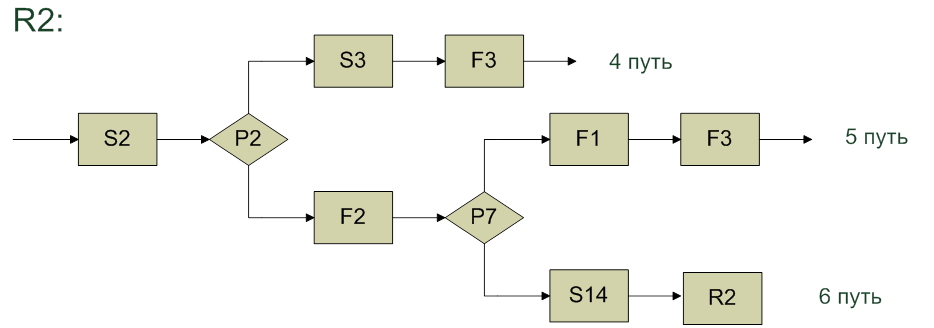
4 путь:
P2(S2(X)) ΛY=F3(S3(S2(X)));
P2![]() S2(X) →Y=F3
S2(X) →Y=F3![]() S3
S3![]() S2(X).
S2(X).
5 путь:
![]() P2(S2(X)) Λ P7(F2(S2(X))) Λ
Y=F3(F1(F2(S2(X))));
P2(S2(X)) Λ P7(F2(S2(X))) Λ
Y=F3(F1(F2(S2(X))));
![]() P2
P2![]() S2(X) Λ P7
S2(X) Λ P7![]() F2
F2![]() S2(X) → Y=F3
S2(X) → Y=F3![]() F1
F1![]() F2
F2![]() S2(X).
S2(X).
6 путь:
![]() P2(S2(X)) Λ
P2(S2(X)) Λ ![]() P7(F2(S2(X))) Λ Y=R2(S14(F2(S2(X))));
P7(F2(S2(X))) Λ Y=R2(S14(F2(S2(X))));
![]() P2
P2![]() S2(X) Λ
S2(X) Λ ![]() P7
P7![]() F2
F2![]() S2(X) → Y =R2
S2(X) → Y =R2![]() S14
S14![]() F2
F2![]() S2(X).
S2(X).
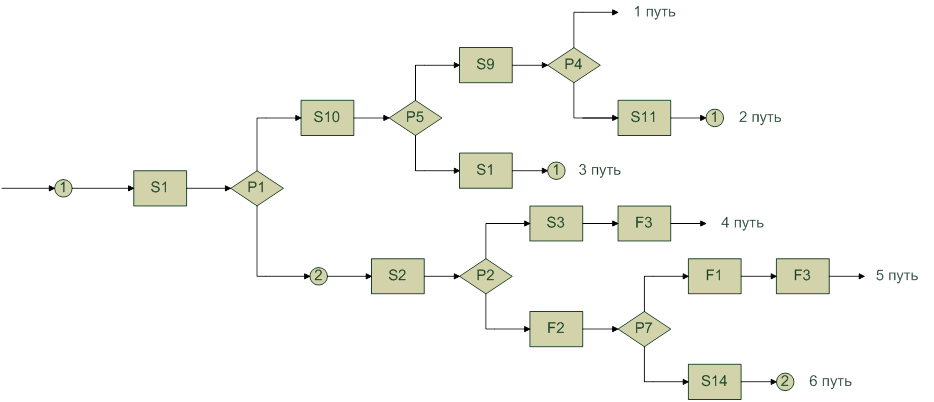
f1={(X,Y)|(P1![]() S1(X)ΛP5
S1(X)ΛP5![]() S10
S10![]() S1(X)ΛP4
S1(X)ΛP4![]() S9
S9![]() S10
S10![]() S1(X)→Y=S9
S1(X)→Y=S9![]() S10
S10![]() S1(X)| P1
S1(X)| P1![]() S1(X)ΛP5
S1(X)ΛP5![]() S10(X)Λ
S10(X)Λ![]() P4
P4![]() S9
S9![]() S10
S10![]() S1(X)→Y=f1
S1(X)→Y=f1![]() S11
S11![]() S9
S9![]() S10
S10![]() S1(X) |
S1(X) |
P1![]() S1(X)Λ
S1(X)Λ![]() P5
P5![]() S10
S10![]() S1(X)→Y=f1
S1(X)→Y=f1![]() S1
S1![]() S10
S10![]() S1(X)|
S1(X)|![]() P1
P1![]() S1(X) →Y=f2
S1(X) →Y=f2![]() S1(X))}
S1(X))}
f2={(X,Y)|
P2![]() S2(X)→Y=F3
S2(X)→Y=F3![]() S3
S3![]() S2(X)|
S2(X)|![]() P2
P2![]() S2(X)Λ P7
S2(X)Λ P7![]() F2
F2![]() S2(X)→Y=F3
S2(X)→Y=F3![]() F1
F1![]() F2
F2![]() S2(X)|
S2(X)| ![]() P2
P2![]() S2(X) Λ
S2(X) Λ ![]() P7
P7![]() F2
F2![]() S2(X) → Y =f2
S2(X) → Y =f2![]() S14
S14![]() F2
F2![]() S2(X)}
S2(X)}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.