Решение задачи на вычисление количества бензина для проезда между несколькими городами, страница 2

<цена>::= целое неотрицательное число

<количество – дорог>::= целое неотрицательное число

<список – дорог>::= пробел | пробел <дорога> <список – дорог>

<дорога>::= <откуда> пробел <куда>

<откуда>::=<куда>::= натуральное число в диапазоне от 1 до <количество – городов>

 Внутреннее представление графа

 Для своей задачи я  использовал представление графа с помощью матрицы смежности, где на пересечении i-ой и j-ой вершин, в случае если они смежные, находится стоимость пути из города i в город j, и, если вершины не смежные

находится бесконечность (в случае моей программы бесконечностью является число 10000). Матрица имеет размер NxN, где N- число городов. Так как стоимость проезда из города i в город j может отличаться от стоимости проезда из города j в город i, то матрица не является симметричной относительно главной диагонали. Элементы главной диагонали всегда равны бесконечности (10000), так как не существует дорог, ведущих из города в себя.

 Преимущество представления графа матрицей смежности- имеем прямой доступ к ребрам графа. Недостаток заключается в том, что независимо от числа ребер объем занимаемой памяти равен NxN.

 Для хранения значений стоимости бензина, я использовал одномерный массив B[N]- где N количество городов.

B=(b₁,b₂,…,b_n),  где b_i- стоимость бензина в i-ом городе, i=1,2,…,n

A=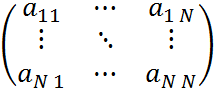

a_ij=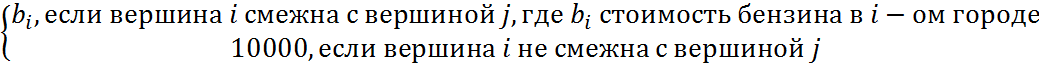

3.2. Выходные данные

 Внешнее представление

rezÎN- стоимость пути или -1, если доехать не возможно и если город единственный

 Внутреннее представление

int rez || -1

4. Укрупненный алгоритм решения задачи

4.1. Укрупненный алгоритм решения задачи

{  ввод числа городов N;

if (N=1) rez←-1

else { Ввод информации о системе дорог и создание матрицы смежности

графа;

Поиск самого дешевого (далее кратчайшего) пути из первого города в последний;

if (кратчайший путь не равен 10000)  rez←кратчайший путь;

else rez=-1;

}

}

4.2. Укрупненный алгоритм ввода системы дорог

{  for (i от 0 до N-1)

for (j от 0 до N-1)

      A[i][j] ←10000

for(i от 0 до N-1)

      ввод стоимости бензина в городе i в соответствующий элемент массива B;

ввод количества дорог M;

for (i от 0 до M-1)                

       { ввод города начала k;

          ввод города конца p;

          A[k-1][p-1] ←B[k-1];

          A[p-1][k-1] ←B[p-1];

        }

}

4.3. Укрупненный алгоритм поиска кратчайшего пути

{  e←0;

if (A[0][N-1]≠ 10000)  rez←A[0][N-1];

else { D[0] ←0;

for (j от 1 до N-1)

      D[j] ←A[0][j];

do 

{ for(i от 1 до N-1)

                { for(j от 1 до N-1)

                      {  if (A[i][j]≠10000)  { if (A[i][j]+D[i]<D[j])  [j]=A[i][j]+D[i];}

       }

                }

        e←e+1;

 }

while (e<N);

rez← D[N-1];

}

}

5. Структура программы

Текст программы содержится в одном модуле.

Модуль (“Main”) содержит главную функцию, функцию ввода матрицы смежности и функцию нахождения кратчайшего пути.

5.1. Состав модуля

 Главная функция main:

- назначение:

определение входных и выходных данных задачи, ввод входных данных, поиск кратчайшего пути и вывод результата.

- прототип функции:    

void main()

Функция Vvod:

-назначение: 

создание матрицы смежности для системы дорог. Функция возвращает указатель на первый элемент матрицы смежности.

- прототип функции:

 int** Vvod (int N, FILE *fp)

- параметры:

N- (входной параметр) количество городов в системе дорог;

fp- (входной параметр) файловая переменная, посредством которой устанавливается связь с файлом с входными данными.

Функция Poisk:

-назначение: