Расчет поля в диэлектрике с помощью теоремы Гаусса

План решения задач по теме «Расчет поля в диэлектрике с помощью теоремы Гаусса»

(by Castbreeder & Zoom)

Варианты формулировок:

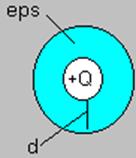
    Дан металлический шар радиусом . Вокруг него слой диэлектрика .
    Толщина слоя . Заряд шарика . Найти потенциал () в центре(на поверхности) шарика(на поверхности диэлектрика, в какой-то точке)...

Решение:

              Во-первых как говорил Баранов можно применить два способа:

1)  через принцип суперпозиции – применим, только если известно распределение зарядов.

2)  через теорему Гаусса – применим, если есть симметрия.

1)  Решается довольно просто – если нужно найти потенциал, то находится E и так как , то через интеграл вычисляется .

Как находится Е – источник заряда разбивается на бесконечно малые элементы. Для которых мы знаем выражение Е(точечные заряды). Находится величина  по заданной формуле. А затем берется интеграл от  по источнику заряда(отрезок, окружность и.т.д.)

2)  Для этого решения используются следующие соотношения:

a)  Теорема Гаусса(в каком-то там виде) -

b)  Определение D :

Для того, чтобы найти потенциал в точке нужно найти разность потенциалов между этой точкой бесконечностью ()

Для того, чтобы найти эту разность нужно взять интеграл(см.выше) .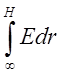

Однако, как нетрудно заметить(как в матане) – эта область неоднородна, значит ее нужно разбить на однородные участки по  - от бесконечности до поверхности диэлектрика(там по умолчанию вакуум - ) - 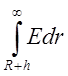, от поверхности диэлектрика до поверхности шара - 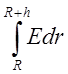 и от поверхности шара до его центра - .

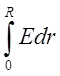Теперь нам нужно найти зависимость , чтобы подставить ее в соответствующие интегралы. Для этого для каждой области:

1)  Выбрать поверхность(сфера, цилиндр), расположенную в интересующих нас пределах.

2)  Определить какой заряд заключен внутри этой поверхности. Если он задан – пишем его, если нет – находим по формуле . Где -объемная плотность заряда(должна быть дана), а  - объем ограниченный поверхностью(сфера - 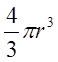, цилиндр - , где - параметр интегрирования)

3)  Пользуясь теоремой Гаусса найдем  - так как для выбранной нами поверхности , то вынесем его за знак интеграла. Обратим внимание, что полученный интеграл -  - есть не что иное, как площадь поверхности(сфера -, цилиндр - , где - параметр интегрирования), а величина есть заряд найденный в предыдущем пункте. Выразим отсюда .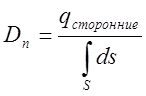

4)  Тогда  будет равно 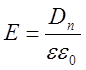. Причем полученное  зависит от параметра .

5)  Вычислим полученный интеграл в необходимых пределах и получим соответствующую разность потенциалов.

6)  Так как потенциал – аддитивная величина, то сложив разности потенциалов по всем областям получим искомую величину.

Замечание: Если необходимо определить , то алгоритм выполняется до пункта 4.

Замечание2: Чтобы найти потенциал(напряженность) в какой-то точке, нужно свести соответствующие поверхности к этой точке. Например если нужно найти потенциал(напряженность)  на поверхности шара, то прибавлять интеграл от поверхности шара до нуля не надо.