Интерполяция в Matlab (отчет по лабораторной)

Федеральное агентство по образованию

РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ

им. П. А. СОЛОВЬЕВА

Факультет радиоэлектроники и информатики

Кафедра электротехники и промышленной электроники

Отчет по дисциплине:

«Научно-технический расчет на ПЭВМ»

по теме

«Интерполяция»

Студенты:                                                                                                     Задоров Д.А.

                                                                                                                       Дубова С.С.                                                                                                                                                                  

Преподаватель:                                                                                              Юдин А.В.

Подпись:

Рыбинск 2010 г.

     Задание №1

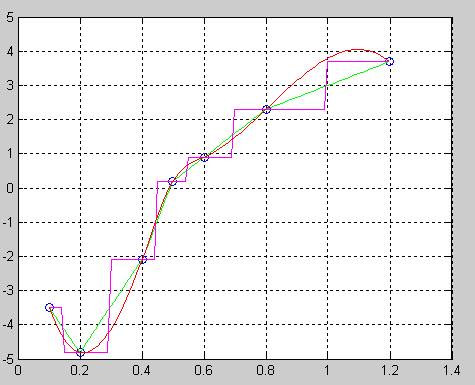
Провести интерполяцию последовательности данных х и у. Интерполировать данную последовательность в интервале xi. В качестве интерполирующей функции использовать interp1 с различными типами интерполяции.

x=[0.1 0.2 0.4 0.5 0.6 0.8 1.2];

y=[-3.5 -4.8 -2.1 0.2 0.9 2.3 3.7];

xi=0.1:0.01:1.2; - сетка интерполяции

yi=interp1(x,y,xi); - интерполируем функцию

yin=interp1(x,y,xi,'nearest') - интерполируем финкцию

yis=interp1(x,y,xi,'spline') -  интерполируем функцию

plot(x,y,'ob',xi,yi,'g',xi,yin,'m',xi,yis,'r') - построение интерполируемых функций и исходных данных

grid;

Задание № 2

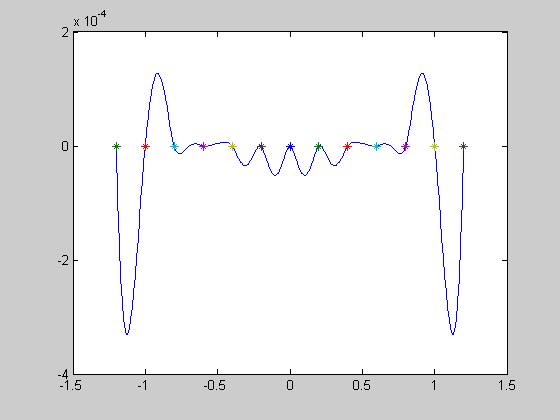
Провести интерполяцию функции у кубическим сплайном на интервале х  при стандартных граничных условиях. Проанализировать полученную структуру. С помощью функции fnval построить график ошибки интерполяции для сетки интерполяции.

x=-1.2:0.2:1.2; - задаем интервал

y=exp(-x.^2); - задаем функцию

xi=-1.2:0.01:1.2; - сетка интерполяции

yxi=exp(-xi.^2); - задаем функцию с учетом сетки интерполяции

s=csapi(x,y); - стандартные граничные условия (задаем сплайн)

s = form: 'pp'

      breaks: [1x13 double]

      coefs: [12x4 double]

      pieces: 12

      order: 4

      dim: 1

yi=fnval(s,xi); - вычисляем сплайн

fnplt(s) - строим график сплайна

Y=yi-yxi - находи погрешность интерполяции

plot(xi,Y,x,0,'*') - строим погрешность, начальные значения в нулевых точках

Задача №3

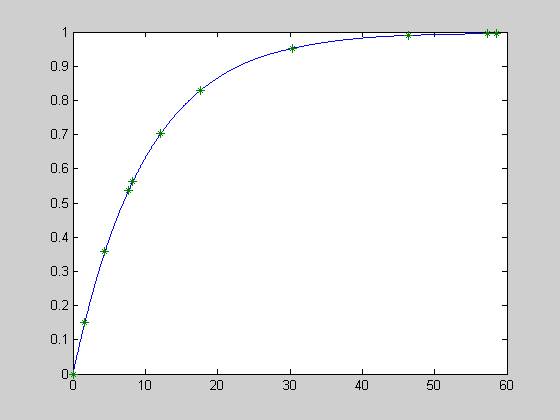
В ходе эксперимента измерялось напряжение U на интегрирующей RC цепочке в моменты времени t. Провести интерполяцию приведенной последовательности данных кубическим сплайном. В одной системе координат построить графики полученной интерполирующей функции, на том же графике отложить исходные данные. Вычислить значение напряжения в момент времени 9 с. Получить структуру сплайна, соответствующего первой производной. По выражению первой производной определить момент времени, когда скорость изменения напряжения станет меньше 0,01.

U=[0 0.152 0.357 0.538 0.563 0.703 0.829 0.952 0.990 0.996 0.997]; -  напряжение

t=[0 1.656 4.417 7.730 8.282 12.147 17.669 30.368 46.380 57.319 58.527]; - моменты времени

ti=linspace(0,58.527,1100) -  сетка интерполяции

s=csapi(t,U); - стандартные граничные условия

sd=fnder(s); - вычисление производную от сплайна

yi=fnval(s,ti) - вычисление сплайна

plot(ti,yi,t,U,'*') - построение сплайна и исходных данных