Поиск длины (числа ветвей) пути от корня до ближайшей вершины заданного непустого бинарного дерева (Лабораторная работа № 3)

Министерство образования и науки

Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра ПМт

Лабораторная работа №3

Тема: «Структуры данных и алгоритмы»

Студент: Трубников А.И.

Факультет: ПМИ

Группа: ПМ-93

Преподаватель: Еланцева И.Л.

Новосибирск 2010

1.  Условие задачи

В заданном непустом бинарном дереве найти длину(число ветвей) пути от корня до ближайшей вершины со значением, равным заданному: при прямом обходе.

2.  Анализ задачи

          Дано:   d-дерево; дерево := (значение, левое дерево, правое дерево)

                   Левое  дерево := дерево|пусто

                   Правое  дерево := дерево|пусто       значениеÎ{символ}

          Результат: min ϵ N, min – минимальная длина до заданного символа.

          Решение: 

Складываем  левое  поддерево в стек, и сравниваем заданный элемент  дерева с элементами из стека. Если нашли равный элементы выдаем сообщение о том, что есть такой элемент, при этом задаем счетчик подсчета уровня (уровень – длина до заданного элемента), на котором находится найденный элемент, и после нахождения прекращаем просмотр левого поддерева. Повторяем эти действие с правым поддеревом. В итоге, если и в правом поддереве нашли заданный элемент, то сравниваем уровни найденных элементов.

Очевидно, что при решении задачи выделяются следующие подзадачи:

1.  Создать пустой стек

2.  Поместить элемент в стек

3.  Взять элемент из стека

4.  Проверить, пуст ли стек

1.  Создание пустого стека

      i=0

2.  Добавление элемента в стек

     a=b

     i=i+1;

3.  Удаление элемента из стека

      если i>0, то

      b=a

      i=i-1

      вывод b

      иначе вывести сообщение об ошибке

4.  Проверка стека на пустоту

     если i>0, то стек не пуст

     иначе стек пуст

3.  Структуры  данных

Внешнее представление входных данных

в файле «in.txt» последовательностью  символов представлено дерево

Внутреннее представление входных данных

бинарное динамическое дерево представлено нелинейным иерархическим списком

Элемент дерева представлен структурой:

struct btree

{ int elem;

btree *left,*right;

}

Внешнее представление выходных данных

выходные данные представлены в виде числа на экране

Внутренне представление выходных данных

int min

4.  Алгоритмы

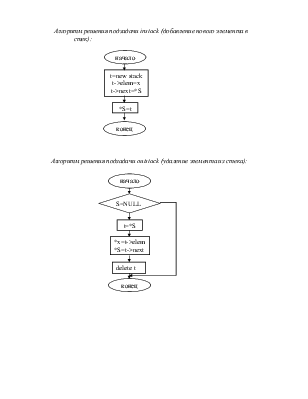
Алгоритм решения подзадачи newstack (создание нового стека):

 

  

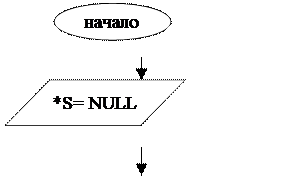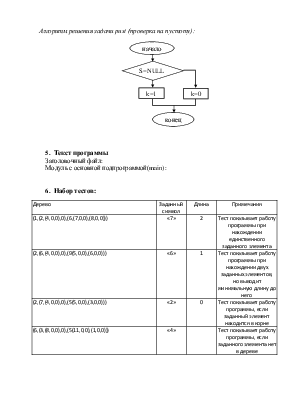
    Алгоритм решения подзадачи instack (добавление нового элемента в

                стек):

              

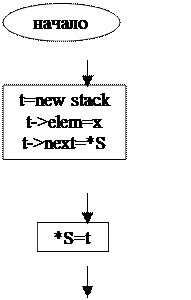Алгоритм решения подзадачи outstack (удаление элемента из стека):

 

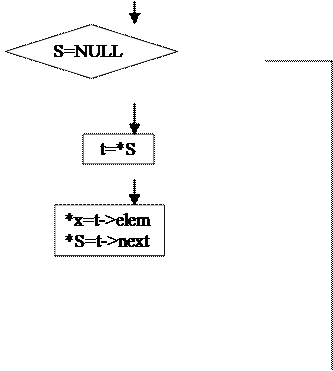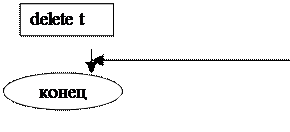Алгоритм решения задачи pust (проверка на пустоту):

k=0

                

 

                  

                       

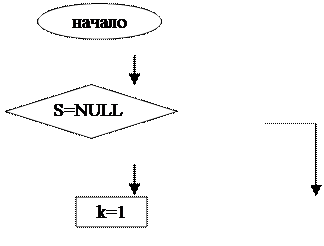5.  Текст программы

Заголовочный файл:

Модуль с основной подпрограммой(main):

6.  Набор тестов:

Дерево	Заданный символ	Длина	Примечания
(1,(2,(4,0,0),0),(6,(7,0,0),(8,0,0)))	«7»	2	Тест показывает работу программы при нахождении единственного заданного элемента
(2,(6,(4,0,0),0),(9(5,0,0),(6,0,0)))	«6»	1	Тест показывает работу программы при нахождении двух заданных элементов, но выводит минимальную длину до него
(2,(7,(4,0,0),0),(5(5,0,0),(3,0,0)))	«2»	0	Тест показывает работу программы, если заданный элемент находится в корне
(6,(3,(8,0,0),0),(5(11,0,0),(1,0,0)))	«4»		Тест показывает работу программы, если заданного элемента нет в дереве

7.  Результаты работы программы:

  Программа выдала желаемый результат на всех тестах.