for(i = 0; i < size; i++) {
p[i]++;
}
}
ftime(&end);
measured = (end.time*1000+end.millitm)-(start.time*1000+start.millitm);
fprintf(out,"%i;%i\n",size,measured);
printf("Measured: %i - %i\n",size,measured);
}
fclose(out);
}
Здесь мы используем массив unsigned char, т.к. в данной реализации С, этот тип занимает ровно 1 байт. Соответственно, размер массива в памяти будет равен числу элементов. Т.к. в Linux нет особого ограничения на выделения памяти, здесь максимальный размер блока определен в 1Мб. Аналогично первому заданию, данные будут сохранены в файле memory.csv.
Проанализируем полученные данные (см. графики 3,4). В итоге, мы имеем, что реально доступно программе (в чистом виде) около 158Кб кэш-памяти процессора.(остальные 98 Кб, видимо, используют сервисные программы). Кроме того, мы наблюдаем еще несколько скачков на графике. Они, видимо, появляются за счет улучшенной технологии кэширования (ATC) и других параметров.
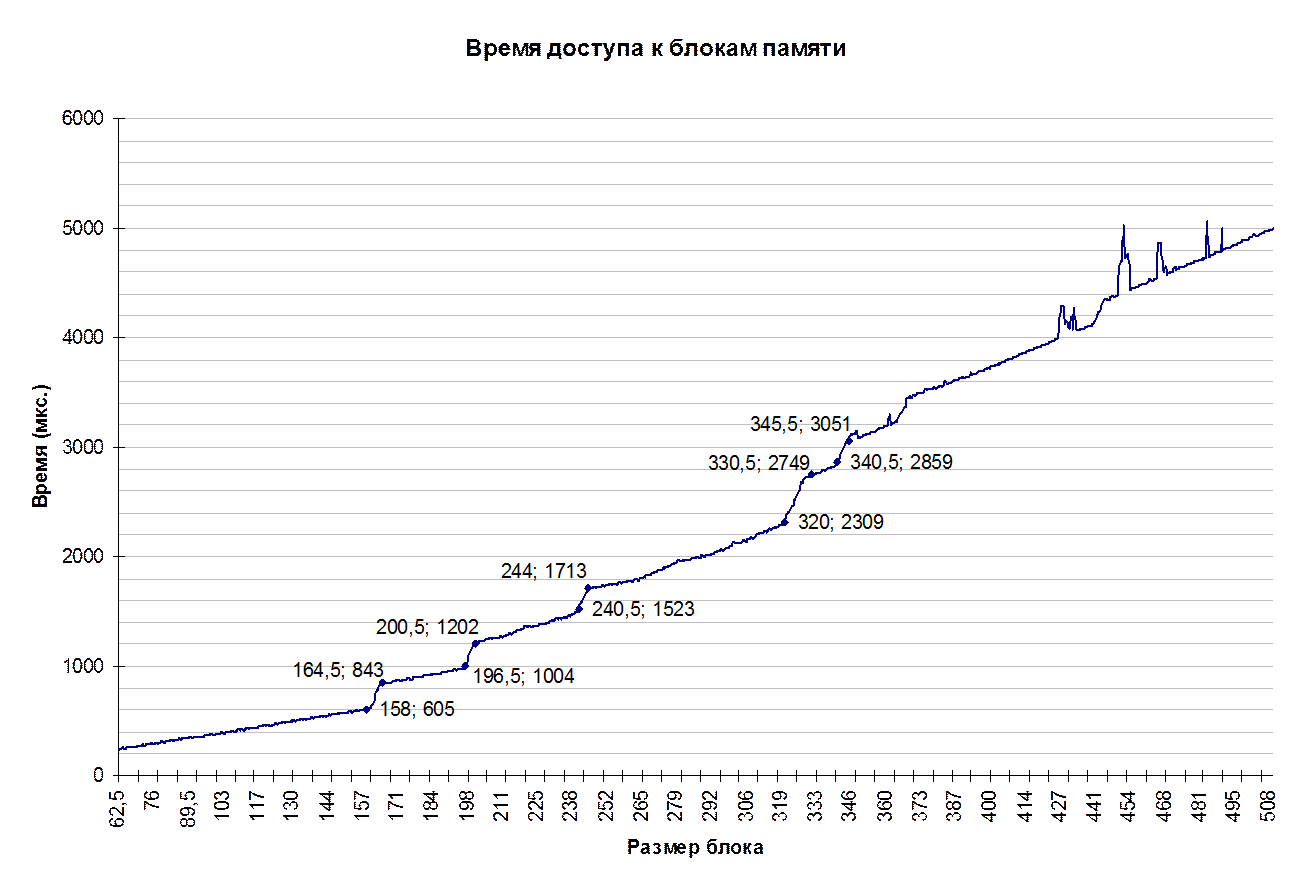
График 3. Время доступа к блокам памяти.
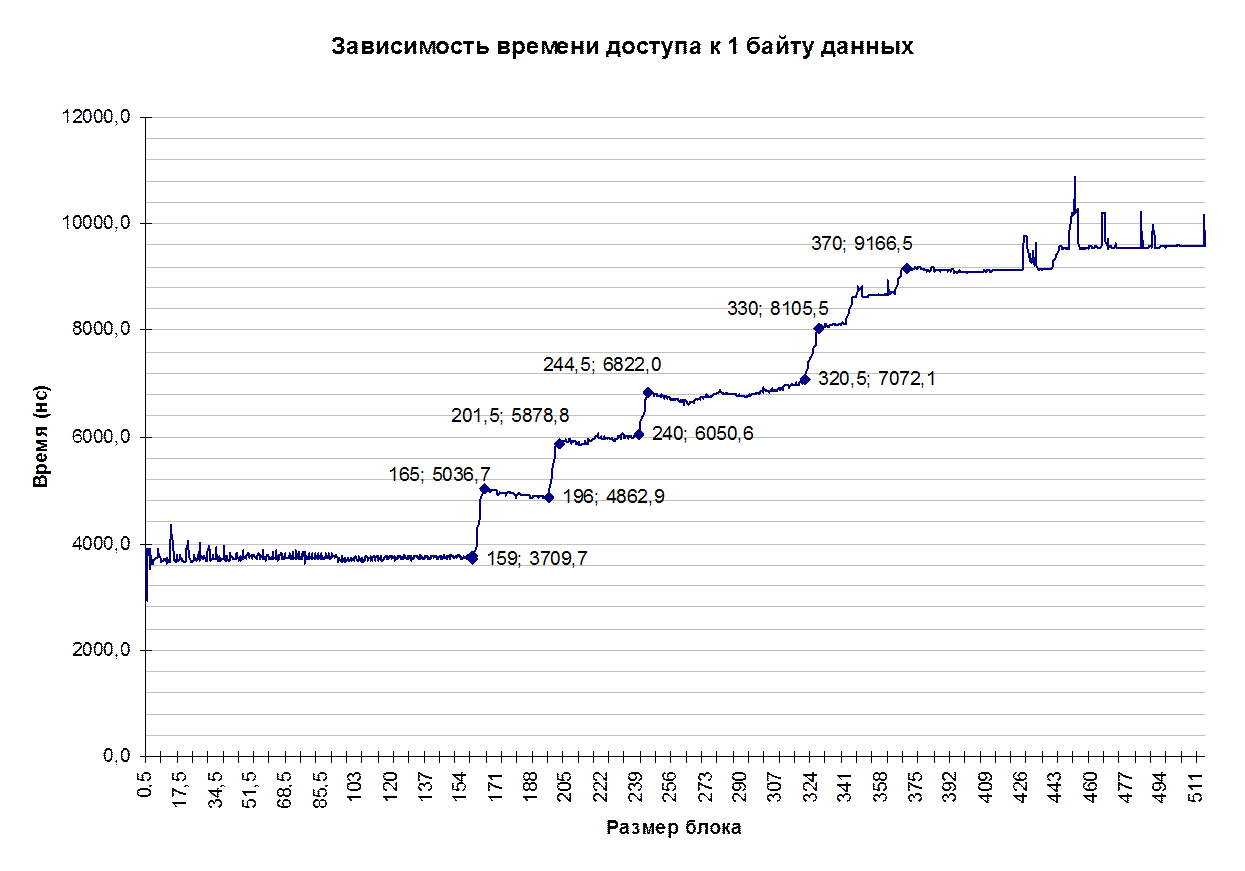
График 4. Время доступа к 1 байту данных из блока памяти.
Эффективное использование иерархической памяти на примере программы умножения матриц
Задача. Написать программу умножения двух квадратных матриц, эффективно использующую организацию иерархической памяти вообще и кэша в частности.
Задание.
1. Написать программу умножения двух квадратных матриц. Программа строится на двух вложенных циклах. Внешний пробегает по строкам первой матрицы и соответствующим им столбцам второй матрицы. Во вложенном цикле идет итерация по всем элементам выбранных во внешнем строк и столбцов. Добавить в программу код для замера времени умножения.
2. Осуществить замеры времени умножения для размеров матрицы от 100 до 1000 с шагом 100, сделать выводы, при каких размерах матрицы полностью умещаются в первичном, вторичном кэшах.
3. Меняя порядок вложенности трех циклов в базовом варианте программы умножения и перебирая нормальное и транспонрованное представления умножаемых матриц, найти наиболее быстрые варианты. Дать им объяснение с точки зрения организации памяти.
Решение.
Т.к. под
управлением ОС Linux нет явного
ограничения на объем используемой памяти, то будем последовательно умножать
матрицы unsigned char’ов начиная с 0х0 до 512х512 с шагом 4 для наилучшей
точности. Сначала мы умножим матрицу М1 на матрицу М2 по правилам линейной
алгебры, т.е. строку на столбец. Затем транспонируем матрицу М1 и умножаем М1
на М2(столбец на столбец). Наконец, транспонируя теперь обе матрицы, умножаем
М1 на М2 транспонированную (строка на строку). На графиках 5,6 явно видно, что
третий результат дает наибольший выигрыш во времени, т.к. структура КЭШе
позволяет производить доступ к переменным, записанным в одной строке (в памяти
и, соответственно, в самом кэше) намного быстрее, чем к тем же переменным,
записанным в столбцы. Оценивая время, затраченное на умножение матриц,
получаем, что средний объем матрицы, полностью умещающейся в первичном кэше: (график
5) около 15 КВ, во вторичном (график 6): 121КВ
Листинг 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.