




Министерство Образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра прикладной математики
Лабораторные работы по дисциплине:
«Архитектуры ЭВМ и ВС»
Факультет : ПМИ
Группа : ПМ22
Студент : Сидельников А.М.
Преподаватель: Маркова В.П.
Новосибирск
2003
Введение.
Тестирование проводилось на компьютере со следующей конфигурацией:
1. Определение реально доступной программе памяти
Задача: Определить максимальный размер массива, целиком умещающегося в кэше, в оперативной памяти.
Решение:
Для решения поставленной задачи используем тот факт, что при обращении процессора к каким-либо данным в памяти они попадают в кеш, и в дальнейшем, если они опять понадобятся, обращение будет происходить к кэшу.
Последовательно выделяя блоки памяти, мы будем изменять их содержимое, и измерять время, которое мы на это затратили. Пока данный блок умещается в памяти определённого уровня иерархии, при увеличении размера блока время доступа растет линейно, когда же его размер станет превосходить размер данной памяти, то это сразу же резко отразится на времени доступа.
Текст программы:
#include <stdio.h>
#include <sys/timeb.h>
#include <stdlib.h>
int S[1024*1024];
void main() {
FILE * out = fopen("memory.csv","wt");
timeb start, end;
int i,times;
long int measured=0;
for(int size = 512;size<=1024*1024;size+=512) {
ftime(&start);
// предварительная запись в кеш
for(i = 0; i < size; i++) {
S[i] = 0;
}
// основной цикл
for(times = 0;times<1000;times++) {
for(i = 0; i < size; i++) {
S[i]++;
}
}
ftime(&end);
measured=(end.time*1000+end.millitm)-(start.time*1000+start.millitm);
fprintf(out,"%i;%i\n",size,measured);
printf("Measured: %i - %i\n",size,measured);
}
fclose(out);
}
По результатам работы программы построим график зависимости времени от размера блока и зависимость скорости доступа от размера блока.
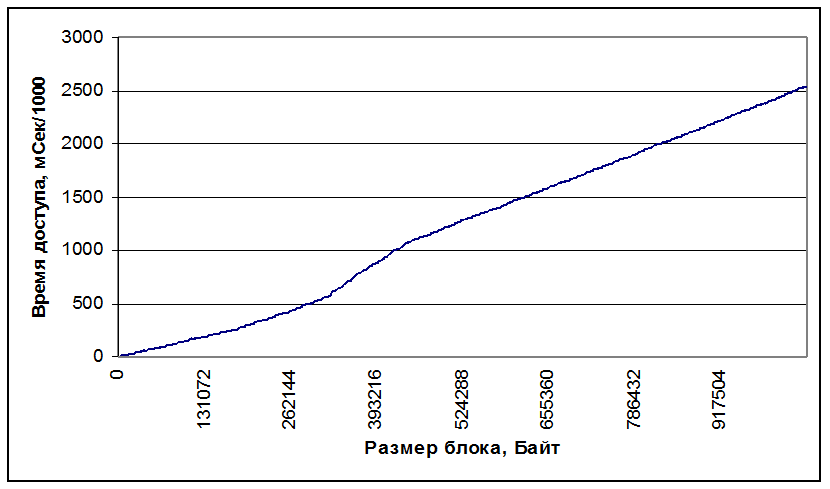
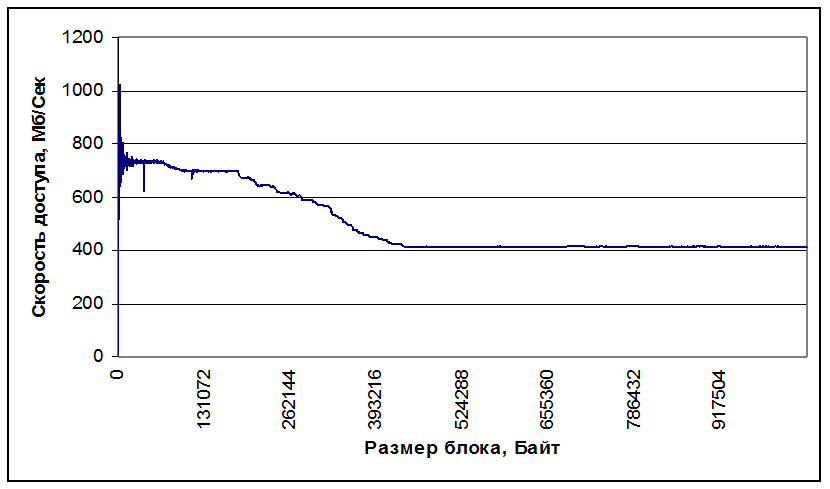
На графиках видно, что при размере блока до 65Кб (кэш L1) достигается максимальная скорость доступа к памяти, затем происходит падение, линейный участок до 183Кб( кэш L2), затем падение и дальнейшая работа происходит с памятью.
Вывод:
При написании программ следует учитывать особенности данной архитектуры чтобы «выжать» максимум скорости выполнения вычислений.
На графике так же видно, что кеш L2, «как бы кончается» на 183Кб, что объясняется тем, что его часть постоянно занята операционной системой.
2. Эффективное использование иерархической памяти на примере программы умножения матриц
Задача: Написать программу умножения двух квадратных матриц, эффективно использующую организацию иерархической памяти вообще и кэша в частности.
Решение:
Построим программу умножения матриц состоящую из трех частей:
На арифметический результат такое умножение не влияет, за то в памяти компьютера эти матрицы уложены по разному.
Текст программы:
#include <stdio.h>
#include <sys/timeb.h>
#include <stdlib.h>
const int SIZE=512;
unsigned char A[SIZE][SIZE];
unsigned char B[SIZE][SIZE];
unsigned char C[SIZE][SIZE];
void randomize(int s) {
timeb h;
srand(s);
for(int i=0;i<s;i++) {
for(int j=0;j<s;j++) {
A[i][j]=rand()%128;
B[i][j]=A[i][j]%127;
}
}
}
void At(int s) {
for(int i=0;i<s;i++) {
for(int j=0;j<s;j++) {
int k = A[i][j];
A[i][j]=A[j][i];
A[j][i]=k;
}
}
}
void Bt(int s) {
for(int i=0;i<s;i++) {
for(int j=0;j<s;j++) {
int k = A[i][j];
A[i][j]=A[j][i];
A[j][i]=k;
}
}
}
void main() {
FILE * out = fopen("matrix.csv","wt");
int s,i,j,r;
long measured=0;
timeb start, end;
for(s=0;s<=SIZE;s+=4) {
randomize(s);
ftime(&start);
for(i=0;i<s;i++) {
for(j=0;j<s;j++) {
C[i][j]=0;
for(r=0;r<s;r++) {
C[i][j]+=A[i][r]*B[r][j];
}
}
}
ftime(&end);
measured = (end.time*1000+end.millitm)-(start.time*1000+start.millitm);
fprintf(out,"%i;%i;",s,measured);
printf("%i - %i - ",s,measured);
At(s);
ftime(&start);
for(i=0;i<s;i++) {
for(j=0;j<s;j++) {
C[i][j]=0;
for(r=0;r<s;r++) {
C[i][j]+=A[r][i]*B[r][j];
}
}
}
ftime(&end);
measured = (end.time*1000+end.millitm)-(start.time*1000+start.millitm);
fprintf(out,"%i;",measured);
printf("%i - ",measured);
At(s);
Bt(s);
ftime(&start);
for(i=0;i<s;i++) {
for(j=0;j<s;j++) {
C[i][j]=0;
for(r=0;r<s;r++) {
C[i][j]+=A[i][r]*B[j][r];
}
}
}
ftime(&end);
measured = (end.time*1000+end.millitm)-(start.time*1000+start.millitm);
fprintf(out,"%i\n",measured);
printf("%i\n",measured);
}
fclose(out);
}
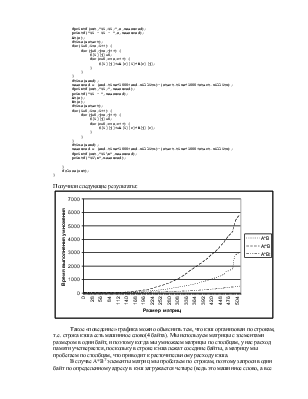
Получили следующие результаты:
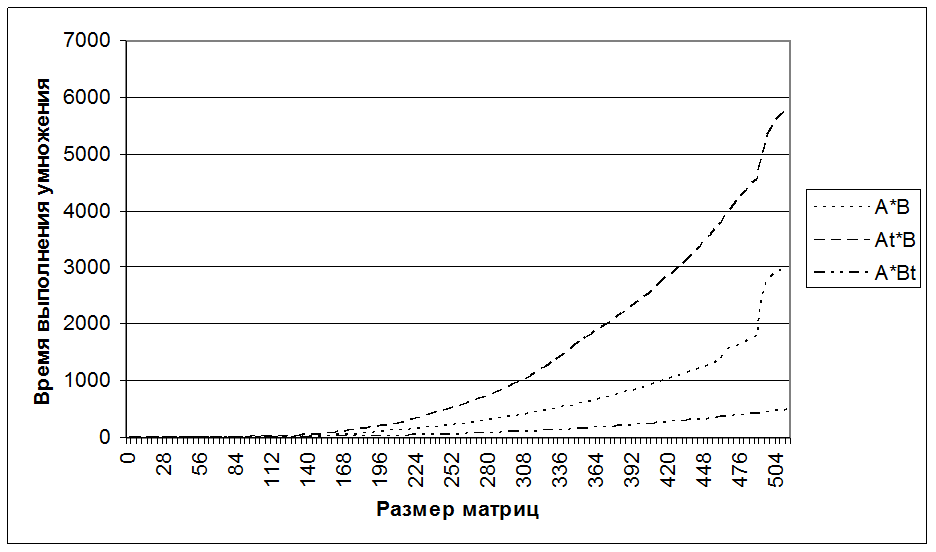
Такое «поведение» графика можно объяснить тем, что кэш организован по строкам, т.е. строка кэша есть машинное слово(4 байта). Мы используем матрицы с элементами размером в один байт, и поэтому когда мы умножаем матрицы по столбцам, у нас расход памяти учетверяется, поскольку в строке кэша лежат соседние байты, а матрицу мы пробегаем по столбцам, что приводит к расточительному расходу кэша.
В случае A*BТ элементы матриц мы пробегаем по строкам, поэтому запросив один байт по определенному адресу в кэш загружается четыре (ведь это машинное слово, а все обмены с памятью происходят с помощью машинных слов) и последующее чтение происходит уже из кэша, а не из основной памяти.
Вывод: Необходимо при разработке программ учитывать внутреннюю структуру кэша, иначе несоблюдение этих мер сразу приведет к резкому падению производительности программы в целом, поскольку будет происходить интенсивный обмен с памятью.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.