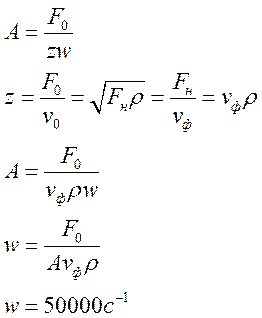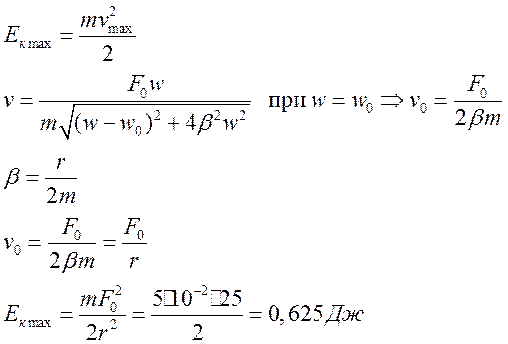
- По струне распространяется
поперечная волна с амплитудой 0.1 см. Максимальное значение ускорения
частиц струны равно 10 м/с2. Разность фаз колебаний двух точек
струны, отстоящих друг от друга на расстоянии 10 см, равна
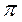 /4. Написать
уравнение волны.
/4. Написать
уравнение волны.
Решение.
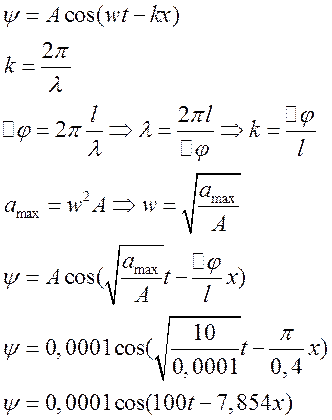
- На тонком стеклянном клине в
отраженном свете (при нормальном падении) наблюдаются интерференционные
полосы. Показатель преломления стекла равен 1.5. Длина волны света 0.58
мкм. Расстояние между соседними темными полосами равно 5 мм. Определить
угол между гранями клина.
Решение.
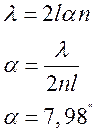
- Период дифракционной решетки
равен 2.8 мкм. Определить наибольший порядок главного максимума и
соответствующий ему угол дифракции для излучения с длиной волны 0.7 мкм.
Решение.
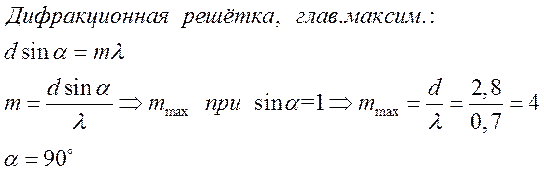
Вариант
8
4. В
колебательном контуре происходят затухающие колебания. L=0,01
Гн, c=1 мкФ, R=120 Ом.
Определить время и количество колебаний, за которое амплитуда уменьшиться в два
раза.
Решение.
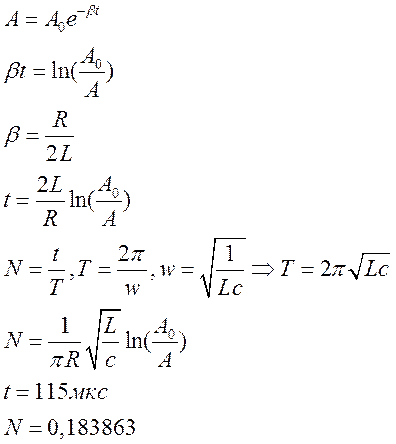
6. В проходящем
свете наблюдается интерфен-я картина, которая получается при нормальном падении
света (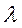 0=0.6 мкм) на тонкий стеклянный
(n=1,5) клин и углом 20’’. Определить расстояние м/у
соседними темными полосами.
0=0.6 мкм) на тонкий стеклянный
(n=1,5) клин и углом 20’’. Определить расстояние м/у
соседними темными полосами.
Решение.
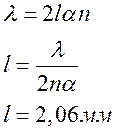
- Происходит дифракция света на
одной щели. Изобразить векторную диаграмму сложения амплитуд в точке
экрана, для которой в щели укладывается ¾ зоны Френеля.
Решение.
Вариант
4.
- Квантовый момент импульса силы.
- Сложить в векторной форме два
однонаправленных гармон. колебания:
X1=4cos(2t+PI/2) и X2=2sin(2t-PI/2).
Изобразить векторную диаграмму. Написать уравнение результирующего
колебания.
Решение.
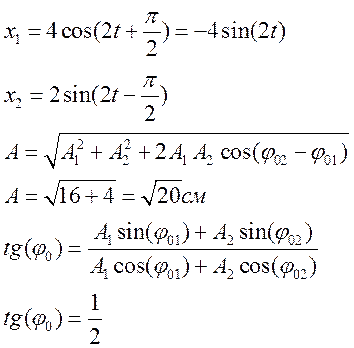
- материальная точка массой m=0,12 г совершает гармонические колебания. Проекцию
ускорения точки меняется по закону ax=0.1sin(4t) м/с2.
Определить максимальное значение смещения и кинетической энергии.
Решение.
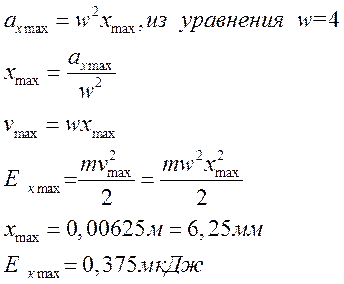
- В колебательном контуре
происходит затухающ.колебания. Параметры контура: L=0.01
Гн, с=2 мкФ, R=50 Ом. Определить время и
количество колебаний, за которое энергия уменьшается в 2 раза.
Решение.
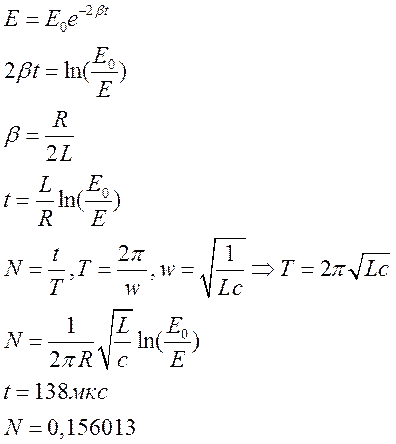
- Вдоль струны распространяется
поперечная гармоничес. Волна с частотой 200 Гц. Линейная плотность струны
0,1 г/м. Сила натяжения 5 Н. Определить расстояние между точками струны,
разность фаз колебаний которых равна PI/4.
Решение.
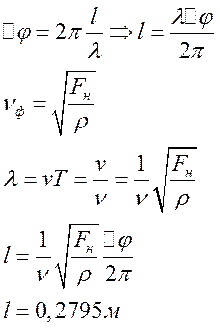
- Сколько светлых полос
уместиться на двух погонных см.поверхности стеклянного клина (n=1,6) если свет (
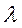 0=0.57
мкм)падает на клин нормально, а интерференц. картина рассматривается в
проход света? Угол клина 24 градуса.
0=0.57
мкм)падает на клин нормально, а интерференц. картина рассматривается в
проход света? Угол клина 24 градуса.
Решение.
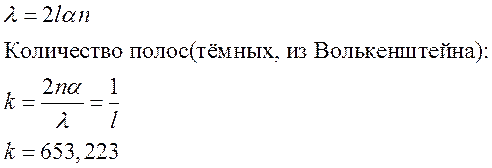
- Происходит дифракция света на
одной щели. Изобразить векторную диаграмму сложения амплитуд в точке
экрана для которой в щели укладывается 3/2 зоны Френеля.
Вариант
1
- Уравнение Шредингера.
Квантово-мех-е описание свободн. Частиц.
- М.т. совершает гармон.колебания
с частотой 20 Гц. Vmax=20 м/с2.
Написать Ур-е колебаний, в начальный момент времени, если в этот (конечный
(?)) момент точка максимально отклонена от положения равновесия.
Решение.
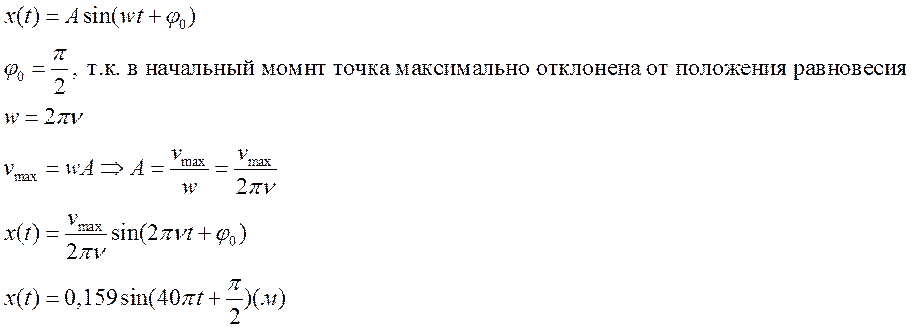
- Поперечная волна на струне
A =0,5 см
Vф=400 м/с. F0=10 Н.
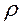 =0.1 г/м.
=0.1 г/м.
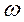 возд?
возд?
Решение.
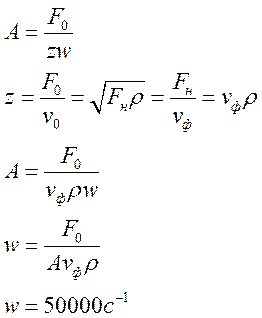
Вариант
3
1) Частица в
одномерной прямоугольной потенциальной яме. Квантование состояний.
2)Материальная
точка совершает колебательние в 2 перпендикулярных плоскостях. x=4cos(2t+Pi/6),
y=2sin(2t-Pi/6). Найти модуль скорости тела в момент времени t=Т/2.
3) Пружинный
маятник, известна частота ню, смещение от положения равновесия, масса груза.
Найти потенциальную энергию тела.
4) Контур с
ЭДС=5В, L=1 мкГн, R=2 Ом, C=1 мкФ. Найти энергию в контуре.
5)
x=Acos(wt-kx). A,w,x - известны.Известна плотность струны ро. Найти импеданс
струны и силу натяжения.
7) Используя
векторное сложение волн получить интенсивность света в максимуме 3го порядка,
если известна интенсивность света во втором максимуме)
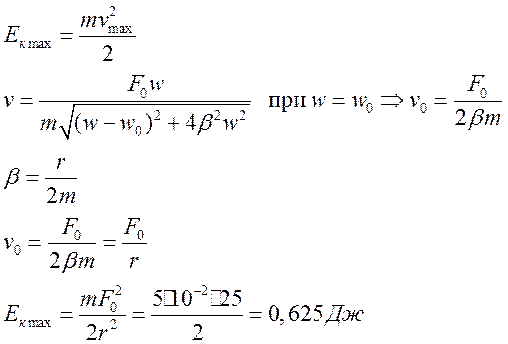
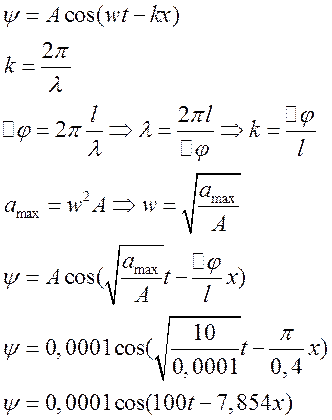
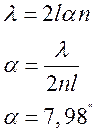
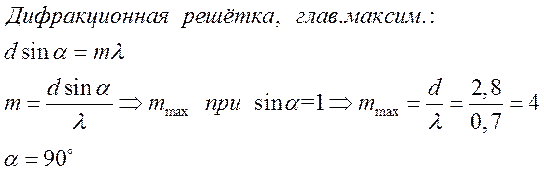
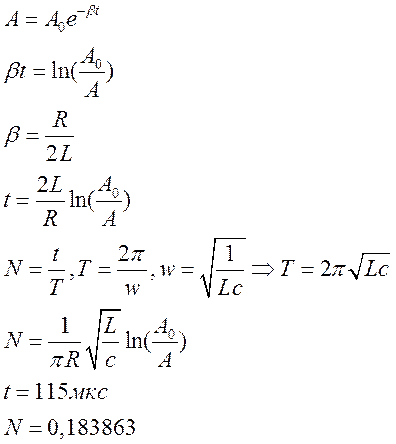
![]() 0=0.6 мкм) на тонкий стеклянный
(n=1,5) клин и углом 20’’. Определить расстояние м/у
соседними темными полосами.
0=0.6 мкм) на тонкий стеклянный
(n=1,5) клин и углом 20’’. Определить расстояние м/у
соседними темными полосами.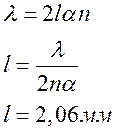
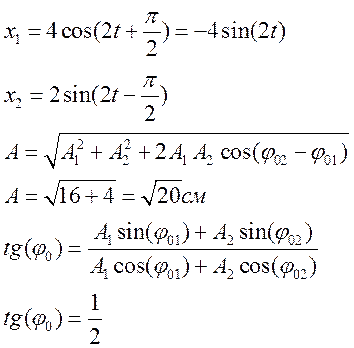
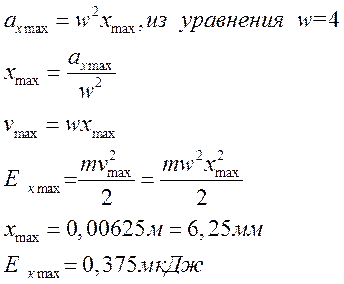
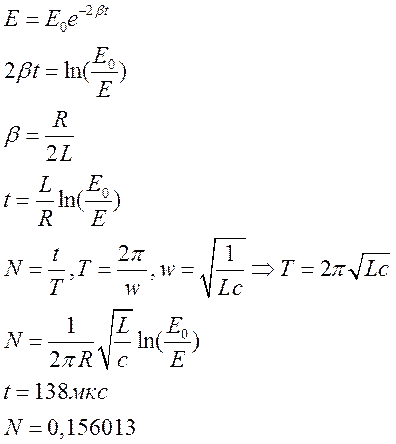
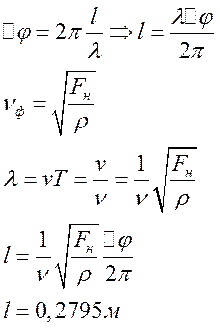
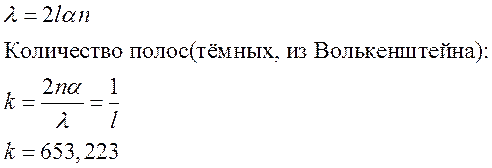
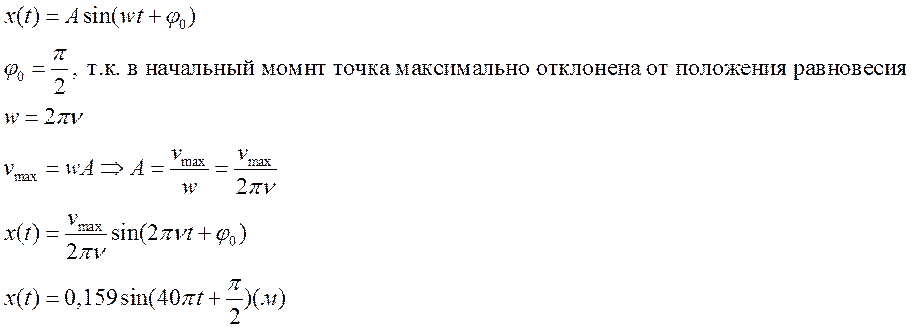
![]() =0.1 г/м.
=0.1 г/м. ![]() возд?
возд?