Выводы по исследованиям:
Все возможные значения смещения порядка
вычисляется по формуле ![]() , где m- количество
бит, отведенные под запись порядка.
, где m- количество
бит, отведенные под запись порядка.
![]()
![]() - искомая степень (положительная)
- искомая степень (положительная)
Аналогично 1), но за счет того, что мантисса может быть представлена в ненормализованном виде (т.е. старший бит равен 0), преобразование идет другим образом. Расширяя значение порядка мантиссы, уменьшается точность (обнуляются числа мантиссы). Это смещение возможно на 23 позиции. Тогда:
![]()
![]() - искомая степень (отрицательная)
- искомая степень (отрицательная)
Число 0.013988227117806674 – число типа DUBBLE, этим объясняется количество значащих цифр. Приведение к типу DUBBLE – инициатива компилятора, возможно, нарушение спецификации FORTRAN77, т.к. переменные, объявленные неявно, не могут быть типы DUBBLE.
Косинусы углов, меньших. 0.013988227117806674, функцией cos() будут равны 1.
Из разложения cos(x) в ряд, имеем:
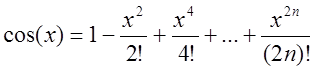
Пусть х=0.0139. Тогда:
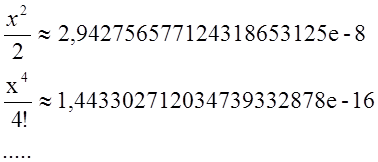
Т.е. слагаемые ряда убывают слишком быстро, чтобы повлиять на переменную типа REAL, поэтому результат равен 1.
Рассмотрим ряд sin(x):
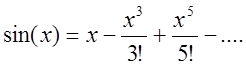
Слагаемые ряда сходятся быстрее, чем у косинуса, но за счет sin(x)=x-…, результат будет отличен от нуля до тех пор, пока угл в представлении в памяти будет отличен от 0.
При переходе от sin() к cos() были использованы следующие соотношения:
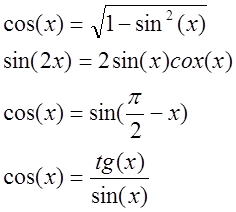
Ни одно из них не изменило значение cos(x)=1.
Таким образом, единственное решение – это расширить диапазон значений, использую переменные типа REAL*8 (вычисление по теореме косинусов не дает большого результат, т.к. при данных входных данных промежуточных вычислении слишком много и потеря точности приводит вновь к cos(x)=1)
Для исследования мы последовательно переводили
(программа прилагается) число ![]() с разным количеством
значащих цифр в двоичный код и сравнивали результат:
с разным количеством
значащих цифр в двоичный код и сравнивали результат:
|
3.14159 |
11.00100100001111110011110 |
|
3.141592 |
11.00100100001111110101111 |
|
3.1415926 |
11.00100100001111110110100 |
|
3.14159265 |
11.00100100001111110110101 |
|
|
11.00100100001111110110101 |
После 3.14159265 мантисса не меняется, а, значит, не влияет на вычисления. Значит, этого достаточно для вычислений.
Программа перевода чисел в двоичную систему счисления:
#include <stdio.h>
int main(int argc, char *argv[])
{
int mx[23],i;
float f;
scanf("%f",&f);
for(i=0;i<23;i++)
{
f=f*2;
if(f>1) {f-=1; mx[i]=1;} else mx[i]=0;
}
for(i=0;i<23;i++)
printf("%d",mx[i]);
return 0;
}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.