stop
endif
if(n*l+2*n+2.gt.1000000) then!proverka na perpolnenie
print *, 'Perepolnenie pamyati'
pause
stop
endif
open(unit=11,access='direct',recl=64,file='x_matrix.bin')!*****************chislo bait
open(unit=12,access='direct',recl=n*4,file='x_vector.bin')
ih=0
im=0
is=0
ims=0
ih1=0
im1=0
is1=0
ims1=0
call Gettim(ih,im,is,ims)
do i=1,n*l/16,1!******************chislo peremennyh
read(11,rec=i) (x_mem(i+j+2),j=0,7) !chitaem AL
enddo
call Gettim(ih1,im1,is1,ims1)
i_time=ims1-ims+(is1-is)*1000+(im1-im)*60000!vremya
print *,'vremya schityvaniya ',i_time
read(12,rec=1) (x_mem(i+n*l+2),i=1,n)
!chitaem vektor
close(1)
close(2)
close(3)
end!input
subroutine multip(n,l,AL,vect,rez)!podprogramma peremnozheniya
integer*4 n,i
dimension AL(l,n),vect(n),rez(n)
ih=0
im=0
is=0
ims=0
ih1=0
im1=0
is1=0
ims1=0
call Gettim(ih,im,is,ims)
do i=1,n
jb=max(1,l-i+1)!otkuda nachinat'
m=max(1,i-l+1)
rez(i)=0
do j=jb,l
rez(i)=rez(i)+AL(j,i)*vect(m)!idem po stroke
m=m+1
enddo
j=l-1
do while(j.gt.0 .and. i+l-j.le.n)
rez(i)=rez(i)+AL(j,i+l-j)*vect(m)!potom po diagonali
m=m+1
j=j-1
enddo
enddo
call Gettim(ih1,im1,is1,ims1)
i_time=ims1-ims+(is1-is)*1000+(im1-im)*60000!vremya
print *,'vremya peremnozheniya',i_time
end!multip
subroutine output(n,rez)
integer*4 n,i
dimension rez(n)
open(4,file='out.txt')!otkryvaem fail
write(4,99) (rez(i),i=1,n)!pishem
99 format(g11.2)
end!output
Program matrix
dimension x_mem(1000000)!vydelenie pamyati
call input(x_mem)!vvod
n=x_mem(1)
l=x_mem(2)
call multip(n,l,x_mem(3),x_mem(n*l+3),x_mem(n*l+n+3)) !sobstvenno schet
call output(n,x_mem(n*l+n+3))!vyvod
print *,'Success'
pause
end!main
4. Тесты, комментарии и примечания
1) «Обыкновенная» матрица. Результат предварительно посчитан на маткаде.
N=5, L=3
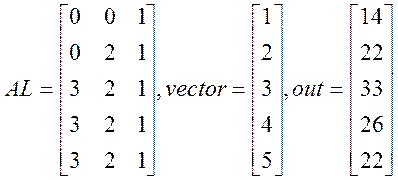
2) Случай, когда максимум полуширины ленты
N=5, L=4
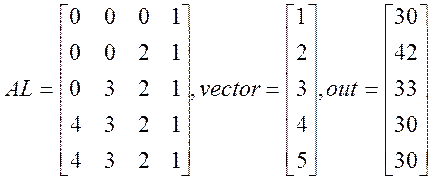
3) Переполнение памяти. Данные хранятся в массиве из 1000 000 элементов, в котором отводится:
- 2 элемента для хранения размерности и полуширины ленты
- N*L элементов для хранения матрицы AL
- N элементов для хранения vector
- N элементов для хранения результата перемножения
Если 2+N*L+2N превышает 1000000, возникает переполнение памяти. Также попутно проверялось условие N>L>0.
N=200 000, L=5
Perepolnenie pamyati!
4) Проблемы с файлами прямого доступа. При работе с файлами прямого доступа следует помнить о том, что количество памяти, вводимое в i-ую запись, не должно превышать заданного при открытии файла параметра recl, определяющего длину записи в байтах.
5) Тестирование на матрицах большой размерности. При тестировании программы заранее был вычислен результат (все ненулевые элементы матрицы равны 1), после проведена серия исследований для матриц различных размерностей. Проблем особых не возникло, вроде.
5. Исследование зависимости времени считывания данных из файла прямого доступа и времени перемножения от размера записи.
|
N |
Время умножения(мс) |
Время считывания файла с прямым доступом(мс). Размер записи (байт) |
||||
|
4 |
8 |
16 |
32 |
64 |
||
|
20000 |
4 |
12 |
7 |
4 |
3 |
3 |
|
50000 |
9 |
31 |
17 |
10 |
7 |
5 |
|
70000 |
15 |
40 |
26 |
15 |
10 |
7 |
|
100000 |
19 |
62 |
34 |
21 |
14 |
10 |
|
130000 |
26 |
76 |
37 |
27 |
19 |
14 |
|
142000* |
27 |
85 |
39 |
29 |
20 |
16 |
* максимально возможная в данном представлении размерность. L=5,
2+2n+5n=10000000, n~142000
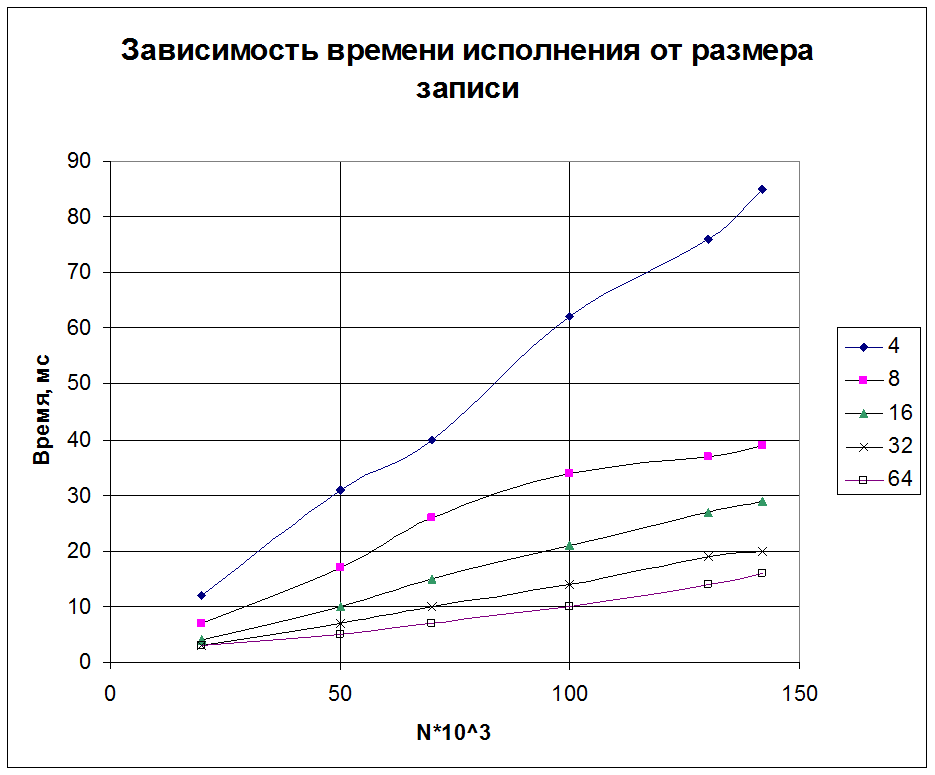
Четко просматривается тенденция: при увеличении размера записи считывание данных проходит быстрее. Объясняется это тем, что, во-первых, программа реже обращается к медленной внешней памяти, и, во-вторых, за одну итерацию получает больше значений переменных, что позволяет быстрее выполнить нужные действия.
В связи с этим был переработан текст модулей, работающих с файлами прямого доступа, и взят максимально возможный размер записи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.