Написание программы, реализующей на языке ФОРТРАН ввод нового треугольника и вычисление площади треугольника

1.  Задача:

Написать программу, реализующую на языке ФОРТРАН вычисление заданного набора геометрических характеристик треугольников с использованием меню. Меню должно содержать следующие пункты:

·  Ввод нового треугольника;

·  Вычисление площади треугольника;

·  Вычисление минимального угла в градусах;

·  Вычисление косинуса минимального угла ;

·  Окончание работы.

Вариант 9:

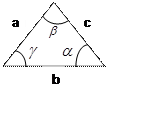
Треугольник задается двумя сторонами и углом между второй и оставшейся стороной.

2.  Входные и выходные данные:

Входные данные: Две стороны и угол между второй и оставшейся стороной (стороны a, b и угол α)

Выходные данные: Площадь треугольника, минимальный угол и его косинус или сообщение об ошибке

3.  Математическая модель:

Существует еще 5 формул для нахождения площади треугольника:

S=  (p(p-a)(p-b)(p-c))^1/2  - 2 неизвестных величины(периметр и 1 сторона);

S=1/2ah_a   - для нахождения высоты требуется найти тригонометрическую функцию угла;

S=pr  - для нахождения периметра требуется найти еще 1 сторону + нахождение радиуса;

S=(abc)/(4R)  - требуется найти еще 1 сторону + радиус.

S=1/2(a*b*sinγ) – требуется найти 1 угол.

Для нахождения площади данного треугольника наиболее оптимальным вариантом является последняя формула, так как она предполагает наименьшее количество действий.

Для проверки корректности данных, а также для нахождения минимального из углов  используем теорему синусов:  a/sinα= b/sinβ = c/sinγ. Из этого равенства следует, что sinβ= (b*sinα)/a, где β – угол, противолежащий стороне b. Тогда, данные стороны и угол будут образовывать треугольник, если b*sinα<a и b>0, a>0, 0<α<180.

Таким образом, проверив данные, мы либо узнаем о некорректности данных, либо находим угол β. Так как сумма углов в треугольнике равна 180, то третий угол γ=180-α-β.Теперь, сравнивая все углы, узнаем, какой из них минимальный. А найденный третий угол используем для вычисления площади треугольника.

4.  Набор тестов:

№	Дано	Результат  (α – мин. угол, S – площадь)	Примечание
1	vvod-> a=5, b=4, α=90, π=3.14159	α =36.87, S=6.0, сos(α)=0.8
2	vvod-> a=-80, b=4, α=30,  π=3.14159	Error (некорректные данные)	Сторона меньше 0
3	vvod-> a=6, b=4, α=-50, π=3.14159	Error (некорректные данные)	Угол меньше 0
4	vvod-> a=6, b=7, α=80, π=3.14159	Error (некорректные данные)	b*sinα>a
5	vvod-> a=0.81237, b=0.54789, α=4.5673, π=3.14159	α =3.078, S=0.029, сos(α)=0.998
7	vvod-> a=1020, b=1020, α=60, π=3.14159	α =60, S=inf, сos(α)=0.5	Переполнение данных
8	vvod-> a=2, b=2, α=60, π=3.14159	α =59.9, S=1.7320499, сos(α)=0.5	После значения числа π=3.1415926, значение площади треугольника не изменяется.
9	vvod-> a=2, b=2, α=60, π=3.141592	α =60, S=1.7320507, сos(α)=0.5
10	vvod-> a=2, b=2, α=60, π=3.1415926	α =60, S=1.7320509, сos(α)=0.5
11	vvod-> a=2, b=2, α=60, π=3.14159265	α =60, S=1.7320509, сos(α)=0.5

5.  Исследования:

Исследование 1:

Равносторонний треугольник со стороной а:

№	Сторона а	Площадь треугольника S

Вывод:

№	Сторона а	Площадь треугольника S

Исследование 2:

Равнобедренный треугольник со стороной

№	Сторона а	cos(α)	Площадь треугольника S
	108

№	Сторона а	cos(α)	Площадь треугольника S
	1010

№	Сторона а	cos(α)	Площадь треугольника S
	1011