![]() ,
,
где
k - постоянная Больцмана, k=![]() Дж/К , EK - средняя
кинетическая энергия, приходящаяся на одну частицу.
Дж/К , EK - средняя
кинетическая энергия, приходящаяся на одну частицу.
Тогда уравнение (1.1) можно записать в виде
![]() , (1.2)
, (1.2)
Или
![]() .
.
Таким образом, применив уравнения классической механики к молекулам идеального газа, мы вывели уравнение его состояния.
Согласно закону Авогадро, моли всех газов занимают при одинаковых условиях одинаковый объем, поэтому для моля вещества константа в уравнении будет одинакова для всех газов:
![]() ,
(1.3)
,
(1.3)
индекс m означает, что данный параметр берется в расчете на моль вещества, R - универсальная газовая постоянная, R=8,31 Дж/(моль∙К)
Для произвольной массы газа m уравнение состояния идеального газа примет вид:
![]()
- уравнение Менделеева – Клапейрона, где μ – молярная масса, ν - число молей (количество вещества).
Отношение ![]() - это постоянная
Больцмана. Здесь
- это постоянная
Больцмана. Здесь ![]() – число Авогадро. Умножим правую часть уравнения (1.3)
на
– число Авогадро. Умножим правую часть уравнения (1.3)
на ![]() . Произведение
. Произведение ![]() равно
числу молекул в массе газа m, тогда
равно
числу молекул в массе газа m, тогда
![]() ,
(1.4)
,
(1.4)
разделив на Vc учетом того, что N/V - число молекул в единице объема, получаем
![]() . (1.5)
. (1.5)
Выражения (1.1), (1.2), (1.4), (1.5) – это уравнения состояния идеального газа.
1.4. Методы измерения температуры.
Абсолютная шкала температур
Из уравнения состояния идеального газа следует, что объем газа пропорционален температуре:
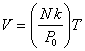 .
.
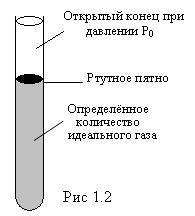
Рассмотрим газовый термометр с постоянным давлением р0 (рис. 1.2). Высота ртутной капли пропорциональна V, следовательно, она пропорциональна T. Если вместо идеального газа взять ртуть, то получим обычный ртутный термометр. С некоторым приближением в этом термометре можно считать T~V.
В случае использования других жидкостей, термометры градуируются по показаниям точных газовых термометров.
Используя идеальный газ, можно построить термометр
с постоянным объемом VO , тогда ![]() .
.
1.5. Гипотеза о равнораспределении энергии по степеням свободы
 Степени свободы -
это число независимых координат, определяющих положение системы, или в
интересующем нас случае — молекулы. Для определения положения центра масс
молекулы необходимо задать три координаты. Это означает, что молекула имеет
три поступательных степени свободы.
Степени свободы -
это число независимых координат, определяющих положение системы, или в
интересующем нас случае — молекулы. Для определения положения центра масс
молекулы необходимо задать три координаты. Это означает, что молекула имеет
три поступательных степени свободы.
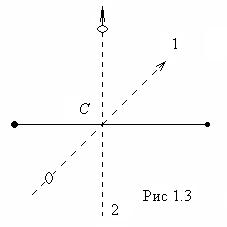
Если молекула двухатомная и жесткая («гантель»), то, кроме трех поступательных степеней свободы, она имеет и две вращательные, связанные с углами поворота вокруг двух взаимно перпендикулярных осей 1-1 и 2-2, проходящих через центр масс С, как показано пунктиром на рис.1.3. Вращение вокруг оси молекулы для материальных точек лишено смысла.
Таким образом, жесткая двухатомная молекула имеет пять степеней свободы: три поступательных и две вращательных.
Если молекула упругая, то возможны колебания атомов и необходима еще одна степень свободы (расстояние между атомами). Ее называют колебательной.
Тот факт, что средняя энергия поступательного движения молекулы равна 3kT/2, означает, что на каждую степень свободы в среднем приходится энергия kT/2. Больцман обобщил этот вывод в виде гипотезы о равном распределении средней энергии по степеням свободы. При этом на колебательную степень свободы должны приходиться в среднем по две половинки kT - одна в виде кинетической и одна в виде потенциальной (как мы знаем, их средние значения одинаковы). Итак, средняя энергия молекулы
![]() ,
,
где i— сумма числа поступательных (Zпост), вращательных (Zвр) и удвоенного числа колебательных (Zкол) степеней свободы: ![]()
Число i совпадает с числом степеней свободы только для жестких молекул.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.