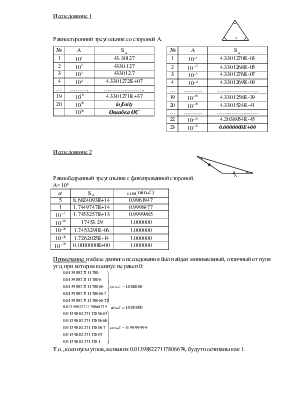
Исследования равностороннего и равнобедренного треугольников

Исследование 1

Равносторонний треугольник со стороной А.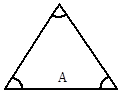                                        

Исследование 2

Равнобедренный треугольник с фиксированной стороной.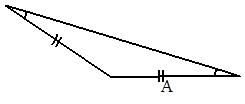  

A=

Примечание: на базе данного исследования был найден минимальный, отличный от нуля угл, при котором косинус не равен 0:

 0.0139882271178066739  

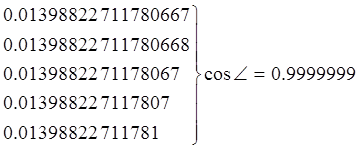
Т.о., косинусы углов, меньших 0.013988227117806674, будут посчитаны как 1.

Исследование 3

Определение количества значащих цифр числа .

Примечание: при использовании функции cosd() (Fortran90) значение косинусов не отличаются от вычисленных функцией cos()(Fortran77), несмотря на необходимость перевода угла в радианную меру.

Вывод: при некоторых значениях исходных данных(слишком больших или слишком малых) искомые величины могут быть найдены неверно. Мы предлагаем 2 пути решения этого:

1. организовать проверку входных данных на принадлежность допустимым значениям. В случае недопустимости выдавать сообщение пользователю о некорректности результата.
2. использовать переменные вещественного типа с двойной точностью. Это не решает проблему, но расширяет интервал допустимых значений.