Изучение методов численного интегрирования (Лабораторная работа № 4)

Министерство Образования и Науки Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра Прикладной Математики

Лабораторная работа №4

По курсу «Программирование вычислений»

Тема «Численное интегрирование»

Факультет ПМИ

Группа ПМИ-51

Студенты:

Казаков С.С.

Карпюк А.А.

Преподаватели:

Рояк С.Х.

Токарева М.Г.

Вариант 5

Новосибирск

2007

1. Цели работы:

Изучение методов численного интегрирования, оценка порядка точности, оценка погрешности по правилу Рунге, уточнение значений по Ричардсону.

2. Условие

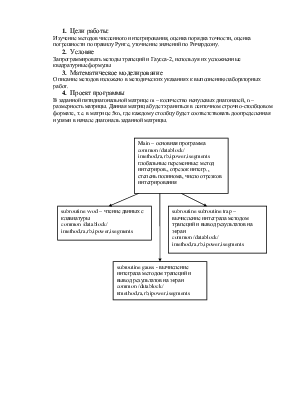
Запрограммировать методы трапеций и Гаусса-2, используя их усложненные квадратурные формулы

3. Математическое моделирование

Описание методов изложено в методических указаниях к выполнению лабораторных работ.

4. Проект программы

В заданной пятидиагональной матрице m – количество ненулевых диагоналей, n – размерность матрицы. Данная матрица будет храниться в ленточном строчно-столбцовом формате, т.е. в матрице 5хn, где каждому столбцу будет соответствовать доопределенная нулями в начале диагональ заданной матрицы.

Main – основная программа common /datablock/ imethod,ra,rb,ipower,isegments глобальные переменные: метод интегриров., отрезок интегр., степень полинома, число отрезков интегрирования

subroutine vvod – чтение данных с клавиатуры common /datablock/ imethod,ra,rb,ipower,isegments

subroutine subroutine trap – вычисление интеграла методом трапеций и вывод результатов на экран common /datablock/ imethod,ra,rb,ipower,isegments

subroutine gauss - вычисление интеграла методом трапеций и вывод результатов на экран common /datablock/ кmethod,ra,rb,ipower,isegments

5. Исследования

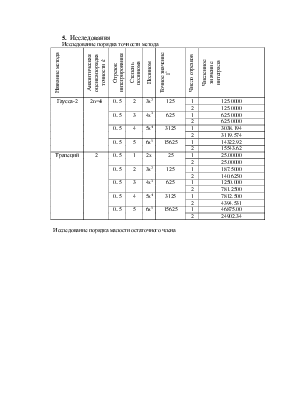
Исследование порядка точности метода

Название метода	Аналитическая оценка порядка точности k	Отрезок интегрирования	Степень полинома	Полином	Точное значение I*	Число отрезков	Численное значение интеграла
Гаусса-2	2n=4	0..5	2	3x2	125	1	125.0000
						2	125.0000
		0..5	3	4x3	625	1	625.0000
						2	625.0000
		0..5	4	5x4	3125	1	3038.194
						2	3119.574
		0..5	5	6x5	15625	1	14322.92
						2	15543.62
Трапеций	2	0..5	1	2x	25	1	25.00000
						2	25.00000
		0..5	2	3x2	125	1	187.5000
						2	140.6250
		0..5	3	4x3	625	1	1250.000
						2	781.2500
		0..5	4	5x4	3125	1	7812.500
						2	4394.531
		0..5	5	6x5	15625	1	46875.00
						2	24902.34

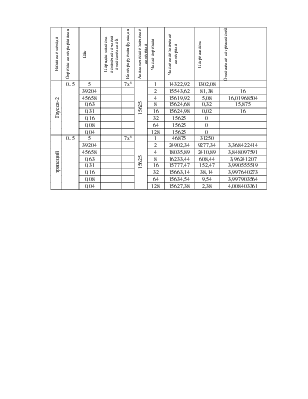
Исследование порядка малости остаточного члена

Название метода	Отрезок интегрирования	Шаг	Порядок малости остаточного члена относительно h	Интегрируемая функция	Аналитическое значение интеграла	Число отрезков	Численное значение интеграла	Погрешность	Отношение погрешностей
Гаусса-2	0..5	5		7x6	15625	1	14322,92	1302,08
		39204				2	15543,62	81,38	16
		45658				4	15619,92	5,08	16,01968504
		0,63				8	15624,68	0,32	15,875
		0,31				16	15624,98	0,02	16
		0,16				32	15625	0
		0,08				64	15625	0
		0,04				128	15625	0
трапеций	0..5	5		7x6	15625	1	46875	31250
		39204				2	24902,34	9277,34	3,368422414
		45658				4	18035,89	2410,89	3,848097591
		0,63				8	16233,44	608,44	3,96241207
		0,31				16	15777,47	152,47	3,990555519
		0,16				32	15663,14	38,14	3,997640273
		0,08				64	15634,54	9,54	3,997903564
		0,04				128	15627,38	2,38	4,008403361