Информатика и выч. техника \ Системы искусственного интеллекта

Игра в Восемь, Изучение основных стратегий решения задач (Лабораторная работа № 3), страница 2

дер-текущее поддерево поиска.

предел- предельное значение f-оценки, при котором допускается решение.

Дер1- дерево дер, расширенное в пределах ограничения предел; f-оценка  дер1 >,чем предел(если только при расширении не была обнаружена целевая вершина).

Решение-решающий путь, ведущий из стартовой вершины через дер1  к целевой вершине и имеющий стоимость, не превосходящую ограничение предел(если такая вершина была обнаружена).

Если ЕстьРеш= «да» , Решение=решающий путь ,найденный при расширении дерева дер с учетом ограничения предел, дер1 =не конкретизировано . Если ЕстьРеш= «нет», дер1=дер, расширенное до тех пор, пока f-оценка  не превзойдет предел, Решение =не конкретизировано. Если ЕстьРеш= «никогда»,дер1 и Решение = не конкретизировано.

After(B,B1,C)-отношение истинно, когда в пространстве состояний существует дуга стоимостью С между вершинами   В и В1.

B1-преемник вершины B;

C- стоимость дуги, ведущей из B в B1.

Aim(B)- отношение истинно, если В- целевая вершина

r(K1,K2,P)-

Р- это «манхеттеновское расстояние » между клетками К1 и К2, равное сумме 2-х расстояний между К1 и К2: расстояние по горизонтали и по вертикали.

Sumr(F1,F2,P)-суммарное расстояние 8 фишек, находящихся в позиции В, от их положений  в целевой позиции.

Ord(F1,F2,I)-степень упорядоченности фишек в текущей позиции по отношению к тому порядку, в котором они должны находиться в целевой позиции.I- вычисляется как сумма очков, приписываемых фишкам: фишка в центральной позиции- 1 очко; фишка  не в центральной позиции, и непосредственно за ней следует (по часовой стрелке) та фишка, какая и должна следовать за ней в целевой позиции F2-0 очков; то же самое ,но за фишкой следует «не та » фишка- 2 очка.

h(B,H)-

H-эвристическаяоценкастоимости оптимального пути из  вершины B в целевую вершину.

H=P+3*I

Max_f(Fmax)-

Fmax  -некоторое значение, задаваемое пользователем , про которое известно, что оно > любой возможной f-оценки.

 


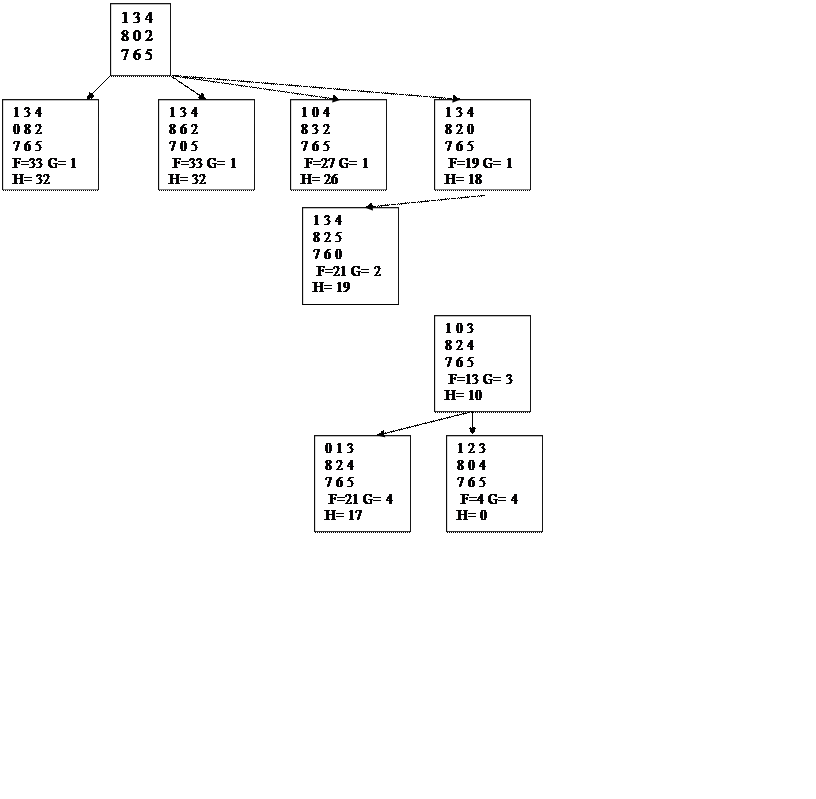
Граф переходов:

 


Решение:

1

1 3 4

8 0 2

7 6 5

2

1 3 4

8 2 0

7 6 5

3

1 3 0

8 2 4

7 6 5

4

1 0 3

8 2 4

7 6 5

5

1 2 3

8 0 4

7 6 5

Текст программы:

domains

      xy = xy(i,i)

      sost = xy*

      i = integer

      way = sost*

      num = num(i,i)

      pair = rang(sost,i)

      allp = pair*

      ver = ver(sost,num)

      list = tree*

      tree =der(sost,num,list );

             ver(sost,num)

      solve = symbol

      sh = sh(symbol,xy)

      sl = sh*

      il = i*

      file = fi1;fi2

predicates

      h(sost,i);

      poisk(sost,way);

      maxf(i);

      broad(way,tree,i,tree,solve,way);

      continue(way,tree,i,tree,solve,solve,way);

      ins(tree,list,list);

      f(tree,i);

      opt_f(list,i);

      min(i,i,i);

      make_next(i,allp,list);

      Help(solve,list,list).   

      member(sost,way);

      aim(sost);

      after(sost,sost,i);

      check(allp);

      bagof(way,sost,allp);

      bagof_(way,sost,allp,allp);    

      need(pair,way,sost);

      member_p(pair,allp);

      member_s(sh,sl);

      member_i(i,il);

      show(way,i);

      showp(sost);

      change(xy,xy,sost,sost);

      r(xy,xy,i);

      r1(i,i,i);

      sumr(sost,sost,i);

      ord(sost,i);

      ord(sost,i,i);

      get_score(sost,i,i);

      get_i(xy,sost,i,i);

      get_xy(i,sost,xy);

      next(xy,xy);

      test(xy,xy,i).

      checker(i,i,i,i).      

clauses

      poisk(Start,Resh):-

            maxf(Fmax),broad([],ver(Start,num(0,0)),Fmax,_,"yes",Resh).

%Fmax > любой f-оценки

      need(rang(B1,C),P,B):-after(B,B1,C),not (member(B1,P)).

      bagof(P,B,L):-bagof_(P,B,[],L).

      bagof_(P,B,A1,A2):-

             need(Q,P,B), not (member_p(Q,A1)),!,bagof_(P,B,[Q|A1],A2).

      bagof_(P,B,A1,A1).

      check([]).

      broad(P,ver(B,_),_,   _,"yes",[B|P]):-

             aim(B).

      broad(P,ver(B,num(F,G)),Lim,Tr1,IsResh,Resh):-

             F<=Lim,

             bagof(P,B,Flwrs),

             not (check(Flwrs)),!,

             nl,write("Parent: "),showp(B),write("Children: "),

             make_next(G,Flwrs,TT),opt_f(TT,F1),

               broad(P,der(B,num(F1,G),TT),Lim,Tr1,IsResh,Resh).

      broad(P,ver(B,num(F,G)),Lim,Tr1,IsResh,Resh):-

             F<=Lim,

               IsResh="never".% нет преемников - тупик

      broad(P,der(B,num(F,G),[T|TT]),Lim,Tr1,IsResh,Resh):-

             F<=Lim,

             opt_f(TT,OF),min(Lim,OF,Lim1),

             broad([B|P],T,Lim1,T1,IsResh1,Resh),

            continue(P,der(B,num(F,G),[T1|TT]),Lim,Tr1,IsResh1,IsResh,Resh).

Скачать файл