

В общем случае, матрица преобразования координат задаётся в виде произведения нескольких сомножителей:
I'=…·M3·M2·M1·I.
Например, можно заказать преобразование фазных величин в
симметричные составляющие по формуле (1.1), заменив ![]() на 3,
как это чаще делают в России. Это можно сделать, домножив матрицу
преобразования (1.1) на скаляр(ную матрицу)
на 3,
как это чаще делают в России. Это можно сделать, домножив матрицу
преобразования (1.1) на скаляр(ную матрицу) ![]() . Обе матрицы
имеются в файле, поставляемом вместе с программой МАСКАРАД, так что нужно будет
лишь указать на необходимость эти матрицы перемножить.
. Обе матрицы
имеются в файле, поставляемом вместе с программой МАСКАРАД, так что нужно будет
лишь указать на необходимость эти матрицы перемножить.
Для описания матриц преобразования координат и их сомножителей отводится отдельный текстовый файл.
Достаточно часто приходится иметь дело не только с прямым, но и с обратным преобразованием, например, не только с переходом от фазных координат к симметричным составляющим, но и обратно. При этом в тестовый файл можно было бы поместить две взаимно обратные матрицы. Однако в этом нет необходимости: в программе предусмотрена возможность вычисления матрицы обратного преобразования по матрице прямого преобразования. Нужно лишь указать, какая из матриц будет фактически использоваться (возможно использование и обеих). Если матрица прямого преобразования прямоугольна, под матрицей обратного преобразования понимается псевдообратная по отношению к ней (см. (1.6) – (1.8)).
Следует иметь в виду, что при выполнении заказа на расчет мощностей в фазах полюсов программе нужны их напряжения. Для их вычисления используется матрица обратного преобразования. (Её использование не нарушает суммарной мощности фаз любого полюса, что же касается полюсных фаз, то корректность расчета их мощностей при использовании прямоугольных матриц может оценить только пользователь – эту задачу нельзя решить формальными методами математики, требуется анализ содержательной стороны.)
Таблица 4.1
Матрица преобразования
36 Имя имя преобразования (любой текст)
3 Обрат "-->" – признак генерации только прямого преобразования;
"<--" – признак генерации только обратного преобразования;
"<->" – признак генерации и прямого, и обратного преобразований
3 КолМат количество перемножаемых матриц преобразования
3 (Адрес) адрес матрицы-сомножителя или преобразования-сомножителя
1 (ТипАдр) способ задания сомножителя:
"#" – ссылкой на ранее описанное преобразование или обратное ему;
не "#" – адресом описания матрицы
Номер обратного преобразования задается путем прибавления к номеру прямого – числа 500.
Матрицу-сомножитель не обязательно описывать как матрицу общего вида, перечисляя все её элементы в виде комплексных чисел. Для вещественной матрицы можно мнимых частей не указывать, не отводя под них места. Если матрица скалярна (k·1), то ее можно задать одним числом k. И, наконец, предусмотрен еще один тип: упакованная матрица инциденций. Остановимся на нем чуть подробнее.
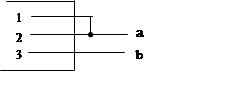
Этот тип удобно использовать для описания схем соединения. Он-то, собственно, и соответствует разъёму в общепринятом смысле этого слова. Так, например, если мы хотим, соединить фазы 1 и 2 3-фазного полюса и подключить их затем к 2-фазному узлу, как показано на рисунке, то закон преобразования токов должен быть таким:
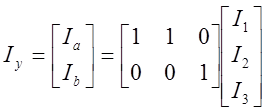 (1.1)
(1.1)
Матрица, описывающая схему соединения, состоящая из единиц и нулей, называется матрицей инциденций. Для нее можно указать лишь расположение единиц, которых бывает обычно немного, а не перечислять, чему равен каждый ее элемент: для каждой единицы следует указать номер строки и столбца, где она расположена. Такой способ описания схем соединения более нагляден.
Таблица 4.2
Первая запись пакета с описанием матрицы-сомножителя
3 Тип тип матрицы:
" :" – комплексная матрица общего вида,
" ." – вещественная матрица общего вида,
" 1" – упакованная матрица инциденций,
" k" – комплексный скаляр
3 Ш ширина поля, отводимого под одно число
3 Строк число строк (выводов со стороны узла)
3 Столб число столбцов (выводов со стороны П,Н)
Таблица 4.3
Записи, начиная со 2-й, для пакета с описанием сомножителя в виде упакованной матрицы инциденций
Ш (i номер строки, где стоит очередная единица
Ш j) номер столбца, где она стоит
Каждая новая индексная пара располагается вслед за предыдущей (на той же строке, если там, конечно, еще есть место). Упорядочивать элементы не нужно. Признаком конца списка служит нулевой номер строки. Об этом следует помнить особенно в том случае, когда собственно список закончился в последней позиции строки: нужно добавить ещё одну пустую строку.
Таблица 4.4
Записи, начиная со 2-й,для пакета с описанием матрицы-сомножителя других типов
Ш*? (MATR) очередной элемент очередной строки
(?=2 для комплексных элементов, ?=1 для вещественных)
Матрицы вводятся построчно: каждая строка – с новой записи.
Для преобразования (1.1) пакет с описанием первого и единственного сомножителя матрицы преобразования мог бы выглядеть, например, в одном из двух приведенных ниже вариантов:
123456789012 123456789012
1 2 2 3 . 2 2 2
1 1 1 2 2 3 1 1 0
0 0 1
Каждый полюс МП подключается к узлу через свой разъём. Пакет разъёмов МП описывается в отдельном текстовом файле. Маска – это тоже разъём.
Таблица 4.5
Пакет разъёмов
3 >> ">> " – признак начала пакета
3 (Разъём) номер разъёма для очередного полюса
1 ; ";" – признак конца пакета
Номер разъёма – это адрес описывающей его матрицы преобразования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.