









Глава2. МЕТОДИКА ГИДРАВЛИЧЕСКОГО РАСЧЕТА
ТЕПЛОВЫХ СЕТЕЙ
2.1. ЗАДАЧИ ГИДРАВЛИЧЕСКОГО РАСЧЕТА
Гидравлический расчет тепловой сети ведут по участкам. Основной задачей гидравлического расчета является определение диаметров трубопроводов d на каждом участке, обеспечивающих пропуск заданного расхода теплоносителя G при заданных потерях давления Dp или напора DН. Также могут быть решены и другие задачи: определение потерь давления Dр или напора DН на участках тепловой сети диаметром d при заданных расходах G, определение пропускной способности G участков трубопроводов диаметром d при перепадах давления на участках Dр или потерях напора DН.
На основании результатов гидравлического расчета участков определяют потери давления или напора по сети в целом, выбирают оборудование, в том числе насосы для водяных и конденсатных сетей, разрабатывают гидравлические режимы.
2.2. ОСНОВЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА
Потери давления на участках теплопроводов складываются из потерь на трение, называемых также линейными потерями DрЛ, и потерь в местных сопротивлениях DрМ:
Dр=DрЛ+DрМ (2.1.)
где DрЛ – потеря давления собственно в трубопроводе;
DрМ – потеря давления при расширениях, сужениях, поворотах трубопровода и в различных устройствах, установленных на участке (компенсаторах, задвижках, клапанах и т.д.).
Рассмотрим более подробно линейные потери давления DрЛ при течении несжимаемой жидкости. Плотность несжимаемой жидкости ρ при изменении давления практически не меняется. При этом условии на участке трубопровода с внутренним диаметром d скорость теплоносителя ω также остается неизменной. В этом случае линейная потеря давления DрЛ определяется по формуле Дарси-Вейсбаха
DрЛ=λ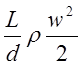 , (2.2.)
, (2.2.)
где λ – коэффициент гидравлического трения;
L – длина участка трубопровода.
При гидравлических расчетах часто используют понятие удельной линейной потери давления RЛ, которая представляет собой линейную потерю давления. отнесенную к единице длины участка трубопровода.:
RЛ=DрЛ/L. (2.3.)
Из уравнений (2.1.) и (2.2.) следует, что
RЛ=λ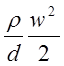 . (2.4.)
. (2.4.)
При ламинарном течении теплоносителя по трубопроводу коэффициент гидравлического трения определяют по формуле Пуазейля-Гагена
λ=64/Re. (2.5.)
Эту формулу используют при Re≤2300. При более высоких значениях числа Рейнольдса, в так называемой переходной области, коэффициент гидравлического трения в гидравлически гладких трубах следует рассчитывать по формуле Блазиуса
λ=0,3164/Re0,25. (2.6)
Большинство труб, используемых для теплоснабжения, с точки зрения гидравлики являются шероховатыми. В переходной области режим течения жидкости в таких трубах определяется не только числом Re, но и величиной относительной эквивалентной шероховатости kЭ/d, которая представляет собой отношение абсолютной эквивалентной шероховатости kЭ к внутреннему диаметру трубы d. Под абсолютной эквивалентной шероховатостью kЭ понимают такую высоту выступов равномерной искусственной шероховатости, при которой коэффициент гидравлического трения получается таким же, как и в реальной трубе.
Значения эквивалентной шероховатости, м, определенные опытным путем для различных видов труб приведены ниже.
Паровые сети……………………………………………………………………0,0002
Водяные тепловые сети ………………………………………………………..0,0005
Тепловые сети горячего водоснабжения и конденсатопроводы…………….0,001
Для расчета гидравлического трения в рассматриваемых условиях наиболее удобна формула А.Д.Альтшуля
λ=0,11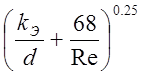 . (2.7.)
. (2.7.)
Эта формула используется
при 10≤Re![]() <500.
<500.
Re![]() <10 она практически совпадает с (2.6.).
<10 она практически совпадает с (2.6.).
При Re![]() ≥500 коэффициент гидравлического
трения λ практически не зависит от Reи определяется только относительной эквивалентной шероховатостью
≥500 коэффициент гидравлического
трения λ практически не зависит от Reи определяется только относительной эквивалентной шероховатостью ![]() , при этом линейная потеря давления DрЛ пропорциональна
квадрату скорости течения ω. Поэтому область Re
, при этом линейная потеря давления DрЛ пропорциональна
квадрату скорости течения ω. Поэтому область Re![]() ≥500 называют областью квадратичного
закона. Поэтому в области квадратичного закона можно определить коэффициент гидравлического
трения по формуле Б. Л. Шифринсона
≥500 называют областью квадратичного
закона. Поэтому в области квадратичного закона можно определить коэффициент гидравлического
трения по формуле Б. Л. Шифринсона
λ=0,11(![]() )0,25 (2.8.)
)0,25 (2.8.)
При Re![]() >500 (2.7.) практически совпадает
с (2.8.).
>500 (2.7.) практически совпадает
с (2.8.).
Получим формулу расчета удельной линейной потери давления RЛ при внутреннем диаметре теплопровода d и пропускной способности участка сети G. Уравнение (2.4.) с учетом уравнения неразрывности
G=ρω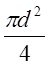 , (2.9.)
, (2.9.)
где G – массовый секундный расход теплоносителя на участке, преобразуется к виду
RЛ=λ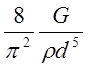 . (2.10.)
. (2.10.)
Отсюда следует, что
d=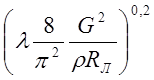 ; (2.11.)
; (2.11.)
G=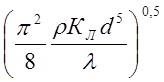 . (2.12.)
. (2.12.)
В зависимости от режима работы теплопровода в уравнения (2.10) – (2.12.)
следует подставлять значение коэффициента гидравлического трения λ из (2.5.) - (2.8.).
Режим работы водяных тепловых сетей чаще всего соответствует области квадратичного закона. В этих условиях (2.10) – (2.12.) с учетом (2.8.) принимают вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.