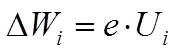 На
свободных концах металла, наряду с внутренней возника- внешняя
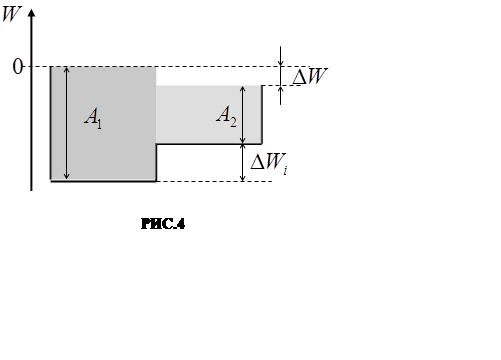
контактная разность потенциалов, появление которой ясно из РИС.4. Когда
металлы приводятся в соприкосно-вение, в контактном слое возникает внутренняя
контактная разность потенциалов Ui , поэтому между основаниями потенциальных
энергетических ям устанавливается некоторая энергетическая разность
На
свободных концах металла, наряду с внутренней возника- внешняя
контактная разность потенциалов, появление которой ясно из РИС.4. Когда
металлы приводятся в соприкосно-вение, в контактном слое возникает внутренняя
контактная разность потенциалов Ui , поэтому между основаниями потенциальных
энергетических ям устанавливается некоторая энергетическая разность
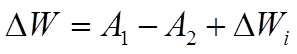 Разность же энергетических уровней между свободными
концами
Разность же энергетических уровней между свободными
концами
В соответствии с этим раз-ность потенциалов между свободными концами
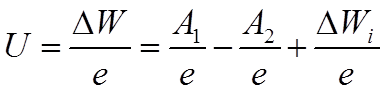 |
или
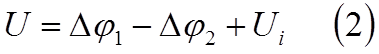 |
Так как Δφ – величина порядка нескольких вольт, а Ui ~ 10-2 – 10-3 B,то за исключением случая, рассмотренного ниже, можно считать
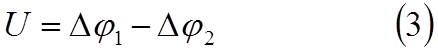 |
Существование контактной разности потенциалов было отк-рыто работами Вольты ещё в XVIII веке. Он установил ряд мета-ллов (ряд Вольты), в котором каждый предыдущий металл при соприкосновении с любым из последующих металлов электризуется положительно. Вот этот ряд:
Al, Zn, Sn, Cd, Pb, Si, Hg, Fe, Cu, Ag, Au, Pt, Pd
Вольта также установил, что если последовательно соединить друг с другом несколько различных металлов, то на концах этого ряда возникает разность потенциалов, не зависящая от промежуточных металлов и равная разности потенциалов при непосредственном контакте крайних металлов.
§ 3. Термоэлектричество
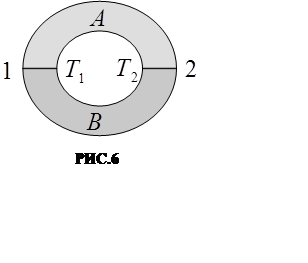
Естественно встаёт вопрос: нельзя ли контактную разность потенциалов использовать для получения электрического тока. На первый взгляд кажется, что достаточно соединить концы А и В (РИС.5), как по цепи потечёт электрический ток.
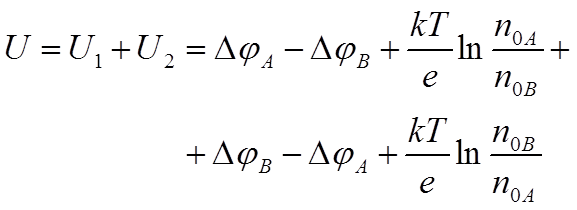
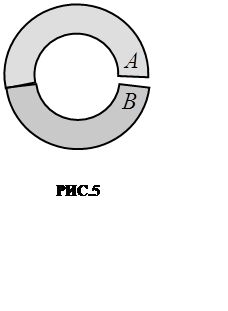 Подсчитаем
сумму контактных разностей потенциалов по всей замкнутой цепи
Подсчитаем
сумму контактных разностей потенциалов по всей замкнутой цепи
Если температура в точках 1 и 2 (РИС.6) одинакова, то это выражение равно нулю, так как
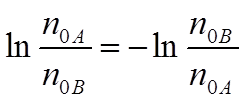 |
В соответствии с рассмотренным выше, ничего не изменится, если эта цепь будет состоять не из двух, а из любого количества разных металлов.
Мы приходим к принципиально важному выводу: в замкну-той цепи, состоящей из проводников только первого рода, су-мма скачков потенциалов равна нулю, если все места контак-тов находятся при одинаковой температуре.
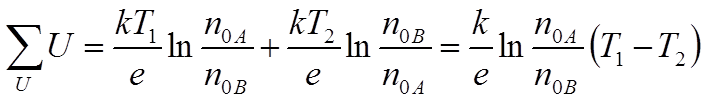 Дело,
однако, коренным образом меняется, если различные контакты находятся при разных
температурах (РИС.6):
Дело,
однако, коренным образом меняется, если различные контакты находятся при разных
температурах (РИС.6):
и в цепи возникает ток. Этот ток существует только при наличии разности температур (Т1 – Т2) , называется термотоком, а суммарная контактная разность потенциалов – термоэлектро-движущей силой. Таким образом, термоэлектродвижущая сила
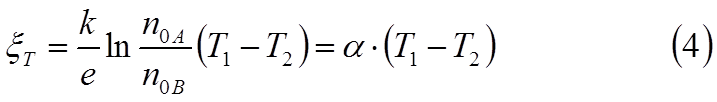 |
Формула (4) носит приближённый характер, так как выраже-ние (1), которое здесь используется, получается на основании классической электронной теории и не является точным. Квантовая теория даёт другое соотношение. Качественно (4) пра-вильно отражает эффект, но зависимость термо-э.д.с. от разности температур в действительности не линейная, а более сложная.
Термоэлектрические явления получили значительное практи-ческое применение. На этом явлении, в частности, основано уст-ройство термопар, применяемых для измерения высоких темпе-ратур и обнаружения малых нагреваний.
Тармопара представляет собой две проволоки из разных ме-таллов, сваренных или спаянных в месте контактов. Один контакт помещается в среду с определённой температурой То (например, в сосуд с тающим льдом), а другой – в среду с темпе-ратурой Т. Если к концам термопары подсоединить чувствитель-ный гальванометр, то он измерит термо-э.д.с., соответствующую разности температур (Т - То). Один раз проградуировав термопа-ру, т.е. установив соответствие между показаниями гальваномет-ра и величинами (Т – То) для последовательного ряда значений Т можно затем использовать термопару как термометр. Промыш-ленность выпускает термопары, гальванометры к которым прог-радуированы уже в градусах. Для большинства пар металлов температура мест контакта почти не влияет на концентрацию свободных электронов, поэтому в (4) α = const и имеет смысл удельной термо-э.д.с., т.е. термо-э.д.с., возникающей при раз-ности температур контактов в 1 градус.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.