Исследование объекта и разработка системы управления перегревателем, предназначенным для нагрева паро-воздушной метанольной шихты, страница 2

Рассмотрим расчёт оптимальной настройки САР по частотным характеристикам и определим закон регулирования и настройки регулятора, на примере  САР температуры паро-воздушной метанольной шихты на выходе из перегревателя (позиция 6), путём изменения подачи в перегреватель (позиция 6), греющего пара.  

Для начала снимаем разгонную характеристику объекта. Для снятия временных характеристик, объект управления приводят в равновесное состояние t₀=110 ^oC, а затем вносят на вход возмущающее воздействие, ступенчатое увеличение подачи расхода греющего пара, перемещением регулирующего клапана (на Δх = 7 % (0,63 кг/ч)  и на основании полученных данных строим разгонную характеристику), в перегреватель (позиция 6). Реакция объекта на это возмущение, кривая разгона, регистрируется в координатах: на осях y(температура), x(время) . Изменение выходной величины регистрируют до тех пор, пока объект управления не примет нового установившегося значения.

Расчетаем передаточную функцию по исходной кривой разгона (см.чертёж    

     МДКП.08.ВАЭ.02.05)  методом Симою.

 

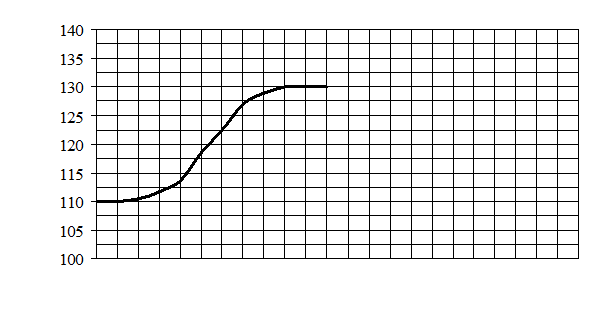                                               Рис.2.1 Кривая разгона

   Расчетная , где- установившееся (максимальное) значение кри-

   вой разгона (рис. 2.1), - текущее значение кривой разгона.

Логарифмируются значения расчетной С и строится график Ln z =  (рис. 2.1 а), (см. табл. 2.2).

,

,

,

пусть ,

то ,

где a = tg b = ln/t.

      Выделяется первая экспонента, с помощью построенной касательной к «хво-    стовой» части полученного графика (рис. 2.2 а).

где  - максимальное значение полученного графика по оси Ln z.

Таблица 2.2 - Экспериментальные и расчетные данные кривой разгона

Время t,мин	Ось у		Ln z	Ось Ln z		Ln z’
		Расчетная С		касательная	С’
0	110	20	3	8	4,95	1,59
1	110	20	3	7	4	1,38
2	110,5	19,5	2,97	6,03	3,06	1,11
3	111,75	18,25	2,904	4,95	2,046	0,71
4	113,5	16,5	2,803	4	1,197	0,17
5	118,5	11,5	2,442	3,05	0,608	-0,49
6	122,5	7,5	2,01	2,02	0,01
7	127	3	1,1	1,1	0
8	129	1	0	0,1	-0,1
9	130	0

Площадь  много меньше площади  (рис. 2.2 а), поэтому продолжаем расчет.

 - площадь «под кривой» графика Ln z,

 - площадь «под кривой» касательной.

Логарифмируются значения полученной С’ и строится новый график Ln z’=                                    

  где Ln z’(t)- это логарифм разности между значениями касательной

  к графику ln z(t) и текущими значениями этого графика С’(см. табл. 2.2).

Выделяется вторая экспонента, с помощью построенной касательной к хвостовой       

  части графика ln z’(t) (рис. 2.2 б).

Площадь  соизмерима с площадью (рис. 2.2 б), т.к.

=5,1 кв.ед.

=4,6кв.ед.

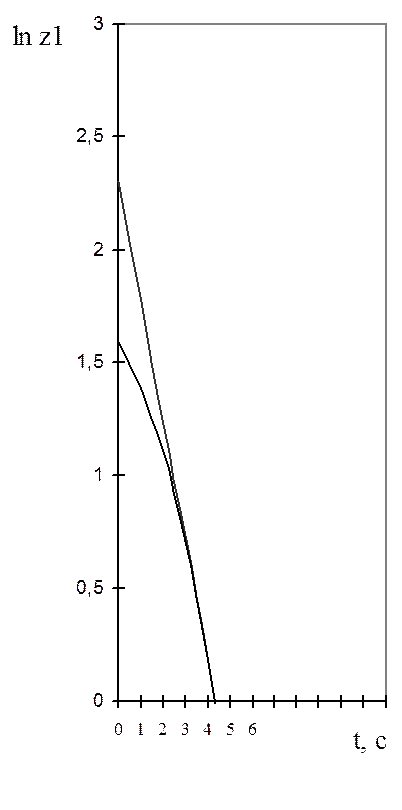
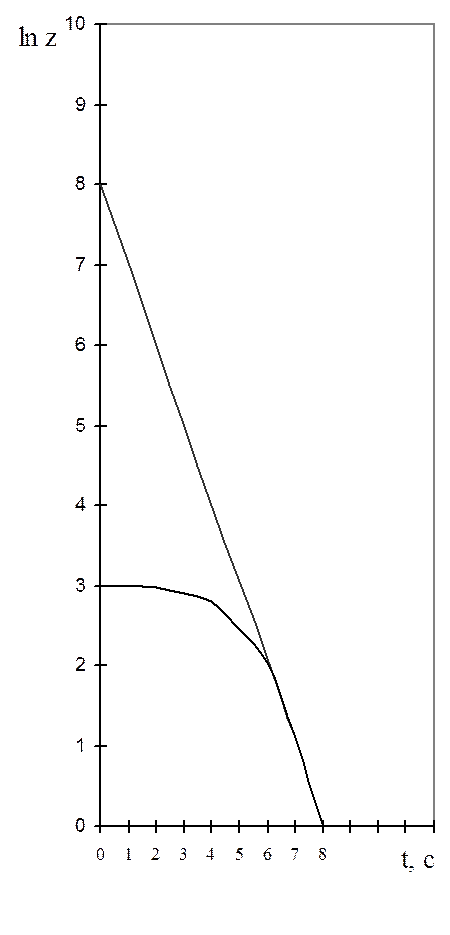
                             а)                       

                                  а)                                                                          б)                                         

Рисунок 2.2 - Расчетные графики

 Объекту присваивается 2-ой порядок, т. е. .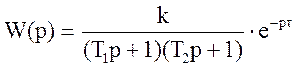

t = 1,4 мин (из рис. 2.1) - запаздывание,

Вычисляется коэффициент усиления объекта k:

.

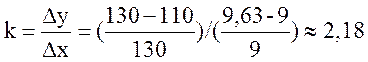Вычисляется значения коэффициентов  и :

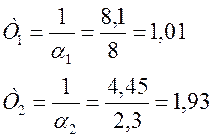
     Находится искомая передаточная функция объекта:

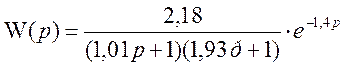                                       .                          (1)                           

Строятся частотные характеристики объекта управления АЧХ и ФЧХ (рис. 2.3),

   которые рассчитываются из формул (2) и (3) соответственно. Результаты расчетов           

   сведены в таблицу 2.3

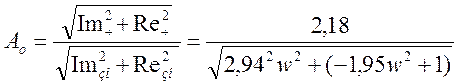,                               (2)

         .                   (3)           

ТАБЛИЦА 2.3- Расчётные данные АЧХ и ФЧХ