Исследование кинематической цепи металлорежущего станка: Методические указания по выполнению практической работы, страница 2

Z = P_а * P_б * P_в = 3*2*2=12

6.3. Числа зубьев шестерен

Подсчитываются числа зубьев каждой шестерни. Правильность подсчетов контролируется проверкой сумм зубьев каждой передачи. Сумма зубьев каждой передачи одной и той же группы в изучаемых приводах с некоррегированными колесами одинакова.

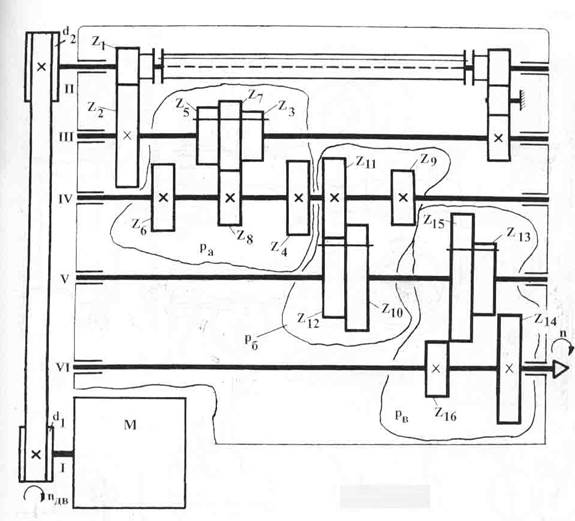
Рис. 1 Кинематическая схема узла:

P_a=3; P_б=2; P_в=2; P_a*P_б*P_в = 3*2*2=12

6.4. Уравнение кинематического баланса привода

Уравнение кинематического баланса привода составляются в трех видах, различающихся формой записи передаточных отношений, входящих в уравнение. Передаточные отношения записываются как i с индексом группы и передачи в данной группе; как отношения обозначений зубчатых колес; как отношения конкретных чисел зубьев колес.

Пример записи уравнений для привода, изображенного на рис. 1:

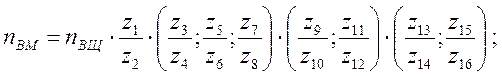
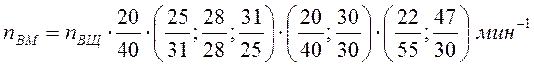
В уравнениях n_ВМ и n_ВЩ – частоты вращения первого и последнего валов привода.
6.5. Расчет передаточных отношений зубчатых передач

Рассчитываются передаточные отношения всех передач, одиночных и групповых, причем передаточные отношения следует записывать в виде   или .

Примеры расчета и записи:

;     ;  ;    ;

             ;          ;     ;

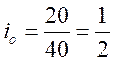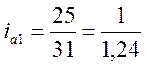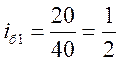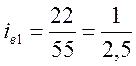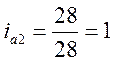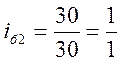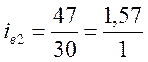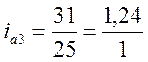
6.6. Установление зависимостей между последовательными передаточными отношениями передач в группах

Устанавливается относительная связь между передаточными отношениями всех передач по каждой группе в отдельности. С этой целью следует разделить второе передаточное отношение группы на первое, третье на второе и т.д. Частные от деления в конкретной группе (обозначим их φ с индексом соответствующей группы) должны быть, во-первых, больше 1, во-вторых, близки по величине между собой, т.е.

в группе P_а          φ = φ_а1 ≈ φ_а2 ≈ …= φ_а.

в группе P_б          φ = φ_б1 ≈ φ_б2 ≈ …= φ_б            и т.д.

При этом φ_а ≠ φ_б ≠…, а меньшее из них (обозначим его φ_мин) близко по величине к какому-либо стандартному значению знаменателя ряда приведенных ниже:

φ

1,06

1,12

1,26

1,41

1,58

1,78

2,0

φ_мин следует принять равным ближайшему стандартному значению.

Пример расчета зависимостей между соседними передаточными отношениями групп передач а, б, в (рис.1):

      

      

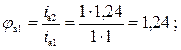
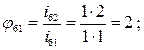
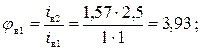
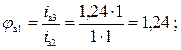
Принимаем φ_мин =1,26.

6.7. Выявление основной и множительной групп в приводе

6.7.1.  Если привод построен по закону геометрического ряда, т.е. обеспечивает на выходном валу геометрический ряд частот вращения со знаменателем φ, то передаточные отношения в каждой группе образуют геометрический ряд со знаменателем φ^x:

Показатель степени при φ, называемый характеристикой группы равен: 

x_o = 1 для основной группы, имеющей P_o передаточных отношений; x₁=P_o для первой множительной группы, имеющей P₁ передаточных отношений,  x₂=P_o * P₁ для второй множительной группы, имеющей P₂ передаточных отношений и т.д.

Итак, знаменатель основной группы φ_o=  φ,

Знаменатель первой множительной группы φ₁=  φ_o^Po ,

Знаменатель второй множительной группы φ₁=  φ_o^{Po* P1}  и т.д.

Вполне очевидно, что φ_o= φ_min и φ_o< φ₁ < φ₂ <… .

Пример проведения кинематического анализа (для рассматриваемого случая: φ_o= φ_min=1,26; x_o = x_a=1 и группа является основной. P_a=P_o=3 .

В первой множительной группе x₁=P_o =3, тогда φ₁= φ_o ^Po =1,26³=2, что равно φ_б.

Таким образом, группа б является первой множительной; P_б=P₁=2 и x_б=3.

Во второй множительной группе x₂=P_o*P₁=3*2=6, тогда φ₂= φ_o ^PoP1 =1,26⁶=4, что примерно равно φ_в =3,93. Таким образом, группа в является второй множительной: P_в=P₂=2; x_в=6.