Фундамент анализа. Последовательности рациональных чисел, страница 2

При доказательстве теоремы единственности мы применили e/2-прием, основанный на неравенстве |a+b| £ |a|+|b|.

4.3. Фундаментальные последовательности рациональных чисел.

Определение. Последовательность (q_n) рациональных чисел называется фундаментальной, если для любого рационального положительного числа e существует такое натуральное число p, что при всех натуральных m и n, больших p, выполняется неравенство |q_m – q_n| £ e.

(" 0 < e Î Q $ p Î N ((" m Î N; " n Î N; m ³ p; n ³ p) Þ |q_m – q_n| £ e)).

Последовательность (2) не является фундаментальной, ибо для любых m Î N любых n Î N q_2m – q_2n+1 = 2.

Вопрос. Фундаментальна ли последовательность (4)? – Нет.

Теорема. Если последовательность рациональных чисел сходится к рациональному числу q₀, то она фундаментальна.

Доказательство.

lim q_n = q₀ Û (" 0 < e Î Q $ p Î N ((" n Î N, n ³ p) Þ |q_n – q₀| £ e/2). Зафиксируем некоторое произвольное положительное рациональное число e, и пусть p = p(e/2) – соответствующее число из определения. Тогда, если m и n – любые натуральные числа ³ p, то |q_m – q₀| £ e/2 и |q_n – q₀| £ e/2, откуда имеем, что для этих же m и n

|q_m – q_n| = | q_m – q₀ + q₀ –  q_n| £  |q_m – q₀| + |q₀ – q_n| £ e/2 + e/2 = e.

Следовательно, последовательность (q_n) фундаментальна. Ч.т.д.

В силу доказанной теоремы нефундаментальная последовательность заведомо не сходится к рациональному числу.

4.4. Постановка задачи.

В связи с только что доказанной теоремой возникает вопрос: всякая ли фундаментальная последовательность рациональных чисел сходится к рациональному числу?

Отрицательный ответ дает пример последовательности (5). Известна

Теорема. Не существует рационального числа, квадрат которого равен двум.

Доказательство. Допустим, что существует несократимая дробь , такая, что ()² = 2, тогда m² = 2n², т.е. m² – четное число, следовательно, и m – четное. Пусть m = 2k, тогда 4k² = 2n². Þ n² = 2k² Þ n² – четное Þ n – четное. Из нашего допущения получили, что m и n делятся на 2, чего быть не может, поскольку  – несократимая дробь.

Рассмотрим квадрат со стороной, равной единице длины. В силу доказанной выше теоремы его диагональ не имеет рациональной длины. Однако, мы всегда можем найти натуральное число р_n так, чтобы удовлетворялись неравенства:

()² £ 2 < (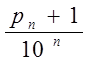)² " n Î N. (*)

В примере (5) q_n = . Покажем, что последовательность () рациональных чисел не сходится к рациональному числу, хотя и является фундаментальной.

Докажем сначала, что lim q_n² = 2. Из правой части неравенства (*) имеем:

2 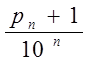– ()² < ()² – ()² = .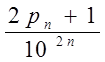

Из левого неравенства (*)

p_n² £ 2×10²ⁿ  < 4×10²ⁿ Þ p_n < 2×10ⁿ.

Тогда  <  =  + .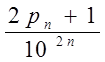

При любом n Î N 10ⁿ > n   Þ  

2 – ()² <  <  + <  + .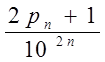

(2 – ()² = 2 – q_n² <  + ) Þ lim q_n² = 2.

Покажем, что (q_n) не сходится к рациональному числу. Допустим, что

lim q_n = q₀ Î Q, тогда из соотношения q_n² – q₀² = (q_n – q₀)( q_n + q₀) следовало бы, что lim (q_n² – q₀²) = 0, т.е. lim q_n² = q₀². Но lim q_n² = 2 Þ q₀² = 2, что противоречит заключению теоремы пункта 4.4.

При этом последовательность из примера (5)  фундаментальна. В самом деле, поскольку lim q_n² = 2 (на основании теоремы пункта 4.3) имеем

" 0 < e Î Q $ p Î N ((" m Î N; " n Î N; m ³ p; n ³ p) Þ |q_m² – q_n²| £ e).

Так как q_m > 1, q_n > 1 на основании соотношения |q_m – q_n| £ |q_m² – q_n²| £ e. ž

Итог. Множество всех последовательностей рациональных чисел разбивается на три класса:

1)  фундаментальные последовательности, сходящиеся в Q;

2)  фундаментальные последовательности, которые не сходятся в Q;

3)  нефундаментальные последовательности; они заведомо не сходятся в Q.

Наша задача: пополнить множество Q такими объектами, чтобы в новом, более широком множестве (É Q) любая фундаментальная последовательность сходилась (имела предел, принадлежащий Q или не принадлежащий Q).