Спектрофотометрический анализ однокомпонентных систем, страница 2

2. Решая совместно (5) и три уравнения (4), относящихся к оптической плотности смеси на одной длине волны но в трёх различных состояниях, получим:

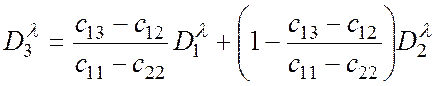 ;                            (7)

где  - концентрация i - того компонента в j-том растворе.

Следовательно, каждый спектр закрытой двухкомпонентной системы может быть представлен как линейная комбинация любых двух других спектров этой же системы, причём сумма коэффициентов линейной комбинации равна единице.

 

3. Подставляя (5) в (4), получим:

.                                             (8)

Составив аналогично уравнения для той же длины волны λ, но для другого состояния системы, и вычитая из него (8), получим:

,                     (9)

где ΔD^λ  - разность оптических плотностей двух растворов, концентрация первого компонента в которых отличается на Δс₁.

Видим, что (9) отличается от известного уравнения для однокомпонентной системы только разностной формой записи. Следовательно, если снимать дифференциальные спектры закрытой двухкомпонентной системы, помещая любой из анализируемых растворов в канал сравнения, то полученное семейство дифференциальных спектров должно удовлетворять всем тестам на однокомпонентность.

С. Открытые двухкомпонентные системы.

Оптические плотности открытой двухкомпонентной системы описываются уравнением (4), но соотношение (5) уже не соблюдаются.

Тесты

1. Решая три уравнения (4) для одного состояния, но трёх различных длин волн, получим:

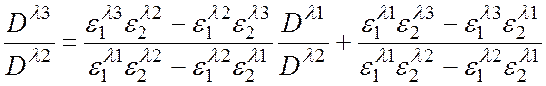
Следовательно, оптические плотности растворов на двух длинах волн, делённые на оптическую плотность тех же растворов на третьей длине волны должны находиться в линейной зависимости.

2. Решая совместно три уравнения (4) для одной длины волны и трёх различных состояний, получим:

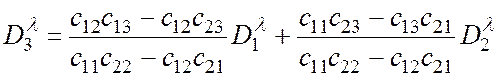 .                           (10)

Следовательно, любой спектр двухкомпонентной смеси может быть представлен как  линейная комбинация двух любых других спектров той же смеси.

3. Разделив обе части (10) на D₂^λ , получим:

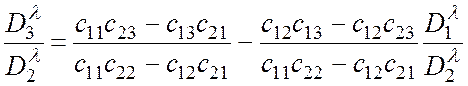                                (11)

Таким образом, оптические плотности двух растворов, делённые на оптическую плотность третьего, должны находиться в линейной зависимости при всех длинах волн.

Известны тесты на трёх- и четырёхкомпонентные системы. Однако они весьма сложны и редко используются на практике.

Количественный спектрофотометрический анализ раствора одного поглощающего излучение вещества (одного компонента) сводится к определению концентрации этого вещества в растворе по известным оптическим плотностям D пробы и стандартных растворов на аналитической длине волны l_ан. При проведении анализа используют следующую последовательность операций:

1.  Снимают полный спектр поглощения пробы и выбирают l_ан . В большинстве случаев l_ан выбирают на максимуме поглощения, поскольку при этом реализуется максимальная чувствительность и воспроизводимость результатов.

2.  Рассчитывают ориентировочное значение e, а с его помощью по уравнению cl= D/e определяют концентрации стандартных растворов анализируемого вещества и толщину кювет. При этом следует иметь в виду, что измеряемые значения оптической плотности должны лежать в диапазоне 0,2 – 1,7, а концентрации стандартных растворов должны перекрывать возможный диапазон концентраций анализируемых растворов.

3.  Готовят 5 – 7 стандартных растворов с известными концентрациями исследуемого вещества и измеряют их оптическую плотность Dпри l_ан .

4.  Строят график зависимости D = f(c) при l = const или D = f(cl), называемый градуировочным графиком анализа или аналитической кривой.

5.  Измеряют оптическую плотность пробы D_x на длине волны  l_ан и по аналитической кривой находят концентрацию анализируемого вещества в пробе с_x.

Рассмотренный графический метод достаточно универсален и может использоваться как при выполнении закона Бугера, так и при его нарушении.

Аналитический метод определения концентрации при выполнении закона Бугера состоит в вычислении с= D/el , где e - коэффициент экстинкции, определяемый на основе измеренных значений оптической плотности стандартных образцов методом наименьших квадратов.

Количественный спектрофотометрический анализ при несоблюдении закона Бугера более трудоемок и менее точен.Во многих случаях нелинейная зависимость D = f(c) может быть с достаточной точностью описана уравнением:

D = a×c + b× c²                                                                  (12)

Коэффициенты этого уравнения вычисляются методом наименьших квадратов по экспериментальным значениям оптической плотности стандартных растворов, после чего концентрация анализируемого вещества в пробе определяется решением уравнения (12).

Порядок выполнения работы

1.  Изучить устройство, оптическую схему и принцип действия спектрофотометра СФ-26.

2.  Провести необходимые измерения для количественного анализа однокомпонентной системы, используя описанную выше методику.

3.  Построить аналитическую кривую, определить концентрацию анализируемого вещества, используя графический метод.

4.  Повторив измерения оптической плотности 7-9 раз, определить погрешность измерения оптической плотности и погрешность определения концентрации.

Литература:

1.  М.Я. Берштейн, Ю.Л. Каминский. Спектрофотометрический анализ в органической химии. Л. 1986.

2.  А.А. Мальцев. Молекулярная спектроскопия. М., 1980.

3.  К.Бенуэлл. Основы молекулярной спектроскопии. М., 1985.