






Лабораторная работа № 13.
РЕЗОНАНС НАПРЯЖЕНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы: изучение условий возникновения резонанса напряжений в колебательном контуре, вычисление индуктивности катушки и расчет добротности контура по ширине резонансной кривой.
Приборы и принадлежности: звуковой генератор, магазин емкостей, магазин сопротивлений, индуктивность, осциллограф С1-73, универсальный прибор В7-35, соединительные провода.
Рассмотрим
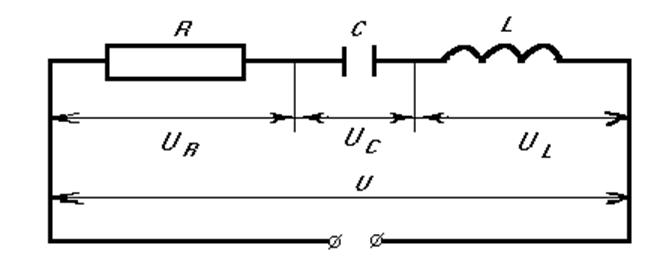
цепь, состоящую из сопротивления ![]() , индуктивности
, индуктивности ![]() и емкости
и емкости ![]() , которые соединены последовательно, и источника
переменного тока (рис. 13.1.) Напряжение в цепи изменяется со временем
гармонически
, которые соединены последовательно, и источника
переменного тока (рис. 13.1.) Напряжение в цепи изменяется со временем
гармонически
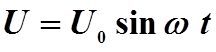
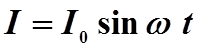 (13.1)
(13.1)
 |
Рассмотрим
каждый участок цепи в отдельности. Для конденсатора получим следующие
соотношения. Если ![]() -
изменение заряда на обкладках конденсатора за время
-
изменение заряда на обкладках конденсатора за время ![]() , то ток равен
, то ток равен
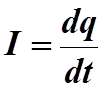 ;
;
![]() ,
,
где
![]() - изменение напряжения на
конденсаторе.
- изменение напряжения на
конденсаторе.
Следовательно,
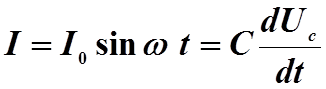 . (13.2)
. (13.2)
После интегрирования находим
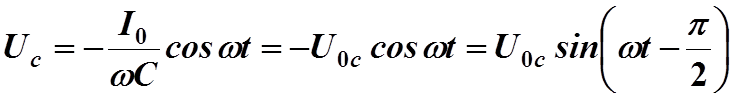 , (13.3)
, (13.3)
или
![]() . (13.4)
. (13.4)
Сравнивая с обычной формулой Закона Ома выражение (13.4), получаем, что величина
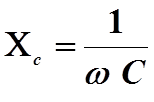 (13.5)
(13.5)
играет роль сопротивления конденсатора переменному току, она называется емкостным сопротивлением.
Из
(13.3) видно, что на конденсаторе напряжение отстает от силы тока на 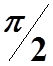 .
.
Физический
смысл такого сдвига фаз заключается в том, что напряжение на конденсаторе
определяется тем зарядом, который находится на нем, а величина этого заряда
определяется током, который протекал через конденсатор несколько раньше, в ![]() предшествующие моменты времени, поэтому
напряжение и отстает по фазе от тока.
предшествующие моменты времени, поэтому
напряжение и отстает по фазе от тока.
Для
омического сопротивления ![]() , которое называется
активным сопротивлением, сдвига фаз наблюдаться не будет, поскольку
, которое называется
активным сопротивлением, сдвига фаз наблюдаться не будет, поскольку
![]()
![]() (13.6)
(13.6)
Обратимся
теперь к индуктивности. При протекании переменного тока через катушку с
индуктивностью ![]() на концах катушки возникает
Э.Д.С. самоиндукции, мгновенное значение которой
на концах катушки возникает
Э.Д.С. самоиндукции, мгновенное значение которой
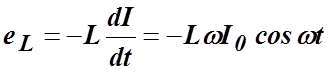 (13.7)
(13.7)
Поскольку возникает Э.Д.С. самоиндукции, то следует применять закон Ома для участка цепи с Э.Д.С.:
![]() .
.
При ![]()
![]()
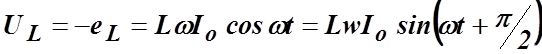 (13.8)
(13.8)
Сравнивая
(13.1) и (13.8), видим, что если в цепи переменного тока включена катушка
индуктивности, активным сопротивлением которой можно пренебречь (т.е. считать ![]() ), то колебания тока в этой катушке отстают
по фазе на
), то колебания тока в этой катушке отстают
по фазе на 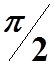 от колебания напряжения в ней.
от колебания напряжения в ней.
При
сравнении (13.8) с законом Ома можно выделить величину ![]() и
рассматривать ее как некоторое индуктивное сопротивление
и
рассматривать ее как некоторое индуктивное сопротивление
![]() . (13.9)
. (13.9)
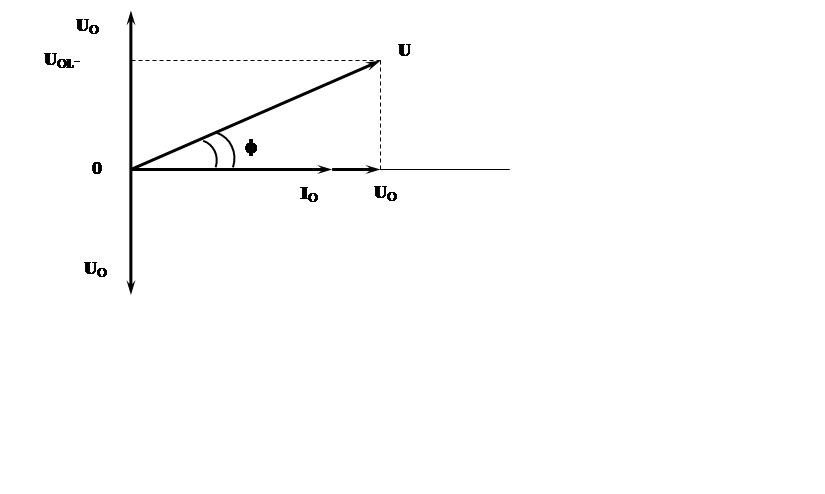
Пользуясь
результатами, полученными выше, построим векторную диаграмму напряжений на
участках ![]() Напряжения на данных участках
представляются на диаграмме векторами
Напряжения на данных участках
представляются на диаграмме векторами
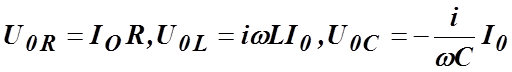 (13.10)
(13.10)
Первый
из них совпадает с осью силы тока ![]() (горизонтальной осью),
а второй и третий повернуты на углы +
(горизонтальной осью),
а второй и третий повернуты на углы +![]() и -
и - ![]() соответственно (на индуктивности напряжение
опережает силу тока на
соответственно (на индуктивности напряжение
опережает силу тока на ![]() ). В результате
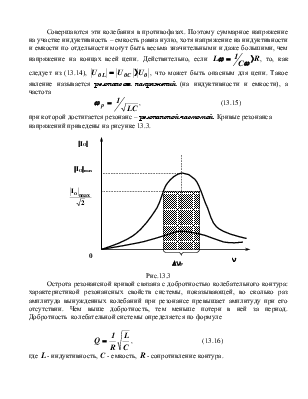
геометрического сложения этих векторов (рис. 13.2) получим вектор
). В результате
геометрического сложения этих векторов (рис. 13.2) получим вектор ![]() , модуль которого определяет амплитуду
напряжения, поданного на весь участок цепи, и угол
, модуль которого определяет амплитуду
напряжения, поданного на весь участок цепи, и угол ![]() -
разность фаз между силой тока и напряжением. Из векторной диаграммы найдем
-
разность фаз между силой тока и напряжением. Из векторной диаграммы найдем
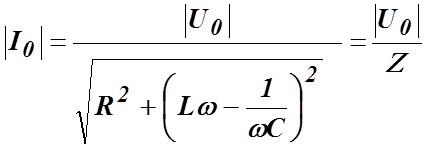 и
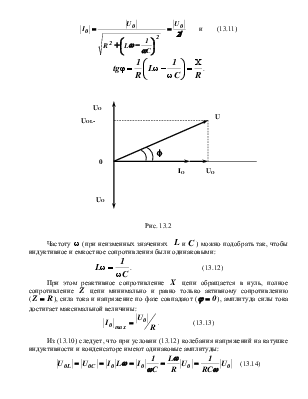
(13.11)
и
(13.11)
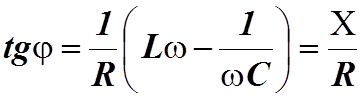 .
.
 |
Частоту ![]() (при неизменных значениях
(при неизменных значениях
![]() и
и ![]() ) можно
подобрать так, чтобы индуктивное и емкостное сопротивления были одинаковыми:
) можно
подобрать так, чтобы индуктивное и емкостное сопротивления были одинаковыми:
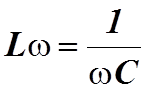 . (13.12)
. (13.12)
При этом реактивное сопротивление ![]() цепи обращается в нуль, полное сопротивление
цепи обращается в нуль, полное сопротивление
![]() цепи минимально и равно только активному
сопротивлению (
цепи минимально и равно только активному
сопротивлению (![]() ), сила тока и напряжение по фазе
совпадают (
), сила тока и напряжение по фазе
совпадают (![]() ), амплитуда силы тока достигает
максимальной величины:
), амплитуда силы тока достигает
максимальной величины:
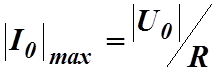 . (13.13)
. (13.13)
Из (13.10) следует, что при условии (13.12) колебания напряжений на катушке индуктивности и конденсаторе имеют одинаковые амплитуды:
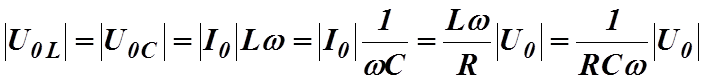 (13.14)
(13.14)
Совершаются эти колебания в противофазах. Поэтому суммарное
напряжение на участке индуктивность – емкость равна нулю, хотя напряжение на
индуктивности и емкости по отдельности могут быть весьма значительными и даже
большими, чем напряжение на концах всей цепи. Действительно, если 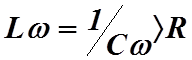 , то, как следует из (13.14),
, то, как следует из (13.14), ![]() , что может быть опасным для цепи. Такое
явление называется резонансом напряжений (на индуктивности и
емкости), а частота
, что может быть опасным для цепи. Такое
явление называется резонансом напряжений (на индуктивности и
емкости), а частота
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.