Ортогональные преобразования системы координат, их классификация. Контравариантные и ковариантные компоненты вектора. Взаимный базис. Способы построения взаимного базиса. Ротор векторного поля

1.  Ортогональные преобразования системы координат, их классификация. Матрица ортогонального преобразования 𝛂. Примеры её построения.

Определение. Ортогональными преобразованиями (ОП) системы координат называются преобразования, оставляющие без изменения квадрат длины вектора, то есть квадрат расстояния между двумя точками пространства.

   Примерами таких преобразований могут служить:

*параллельный перенос системы координат (трансляция);

*вращение;

*отражение координатных осей (инверсия) –изменение направления на противоположное.

  В дальнейшем ОПСК будем описывать матрицей  Матрица  является ортогональной. Напомним, что матрица А называется ортогональной, если транспонированная матрица и матрица , обратная матрице  А, равны:  Покажем, что определитель ортогональной матрицы, в частности матрицы , может принимать только два значения  Действительно

 где единичная матрица. Вычисляя определители обоих частей записанного равенства, получаем

 Отсюда

  Отмеченное обстоятельство позволяет разделить все ОП на две группы:

       - непрерывные ортогональные преобразования (НОП). К ним относятся ОП, определитель матрицы которых . НОП оставляют правую систему координат правой, а левую - левой. Примерами таких преобразований могут служить трансляции и вращения.

       - дискретные ортогональные преобразования (ДОП). Определитель матрицы этих преобразований  ДОП преобразуют правую систему координат в левую и наоборот левую в правую. Простейшим примером такого преобразования является инверсия координатной оси.

  Стремясь максимально упростить поставленную задачу, мы, на начальном этапе, ограничимся изучением вопроса об инвариантности математических объектов только по отношению к НОПСК.

2.  Контравариантные и ковариантные компоненты вектора. Их геометрический смысл. Связь контравариантных и ковариантных компонент вектора.

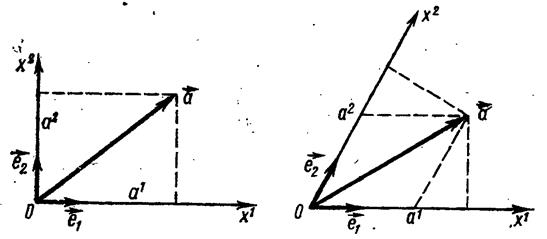
Всякий вектор на плоскости можно разложить на две составляющие по единичным векторам базиса e₁ и e₂:   а=а¹е₁+а²е₂(1)

При этом числа а¹ и а² называются прямоугольными декартовыми координатами вектора а (рис 1).

Если оси координат х¹ и х² не являются взаимно  ортогональными, то вектор а можно задать двояко: разлагая его, как и прежде, по единичным векторам базиса (1), т. е. числами а¹ и а², а также с помощью ортогональных проекций вектора а на оси координат (рис 2).

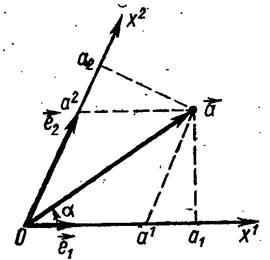
Введем теперь два вектора е₁ и е₂, направленных соответственно по х¹

и х² (рис 3). Тогда для вектора а справедливо соотношение (1). Пара чисел а¹, а² определяет однозначно вектор а. Поэтому эти числа могут быть названы координатами вектора а (контравариантными (по пр. параллелограмма)).

Рассмотрим скалярные произведения (2)

Обозначим длину вектора b через |b|. Тогда из (2) по определению скалярного произведения имеем    (3)

x¹.  Из (2) и (3) имеем

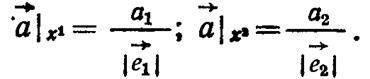
Таким образом, по числам а₁ и а₂ можно определить ортогональные проекции вектора а на оси координат и, следовательно, сам вектор а. Тогда величины a₁ и а₂ тоже можно назвать координатами вектора а, в отличие от предыдущих — ковариантными (по пр. скалярного произведения).

Термин “контравариантный” означает “меняющийся противоположно” чему-либо, а термин “ковариантный” означает “меняющийся аналогично” чему-либо.

             Связь контравариантных и ковариантных компонент вектора.

  По отношению к выбранной косоугольной системе координат вектор  может быть определен (задан) набором своих контравариантных  или ковариантных  компонент. Так как оба набора компонент характеризуют (определяют) один и тот же вектор, то естественно предположить, что они связаны между собой. К установлению этой связи мы и перейдем.

   Используя соотношения  a_i=ae_i (1.2)   и   a=Σaⁱe_i (1.1)   можем записать

                                       (1.3)

где для скалярного произведения орт базиса введено обозначение Выражение (1.3) показывает, что ковариантные компоненты вектора  могут быть представлены в виде линейных комбинаций его контровариантных компонент. Коэффициентами в этих комбинациях в мерном пространстве являются  величин  которые принято записывать в виде квадратной матрицы обозначаемой g. Матрицу g называют фундаментальной матрицей. В частности, в трехмерном пространстве фундаментальная матрица имеет вид

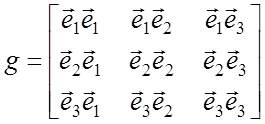                                           (1.4)

   Тот факт, что элементы матрицы g равны скалярным произведениям соответствующих базисных векторов, позволяет сделать следующие выводы о ее свойствах:

   - фундаментальная матрица симметричная   

   - фундаментальная матрица неособенная, то есть

   Так как матрица g неособенная, то существует матрица  обратная матрице g. Обозначим ее элемент . Тогда,

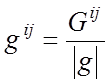где алгебраическое дополнение элемента  определителя матрицы g.

   Умножая матрицы g и ,мы, естественно, получим единичную матрицу

. Используя индексную форму записи, ту же операцию можно записать и «на языке» матричных элементов  .                   (1.5)

Здесь 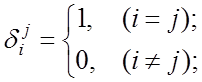      (1.6) - дельта символ Кронекера.

   Покажем теперь, что контровариантные компоненты вектора  можно также выразить в виде линейной комбинации его ковариантных компонент. Умножая обе части выражения (1.3) на и учитывая (1.5), получаем    ,

или       (1.7)

   Выражения (1.3) и (1.7) решают поставленную задачу. Заметим, что в ортонормированной системе координат фундаментальная матрица принимает вид единичной. Следовательно,  то есть контровариантные и ковариантные компоненты совпадают.

 3.  Взаимный базис. Способы построения взаимного базиса