1) метод непосредственного измерения длины твердого тела при повышении температуры, этот метод позволяет найти коэффициент α ;
2) метод интерференционный, которым определяют очень точно изменение длины тела при нагревании, а следовательно, и коэффициент α ;
3) метод дилатометра, служащий для определения коэффициента β у тел неправильной формы;
4) весовой метод, в котором определяется плотность твердого тела при различных температурах с целью нахождения коэффициента β .
Описание установки
Прибор для определения коэффициента линейного расширения твердых тел изображен на рис. 15.1. Исследуемый образец С, имеющий вид стержня, нагревается в воде, находящейся в стеклянной пробирке П. Для нагревания служит нагреватель Н, который включается с помощью кнопочного включателя Д, расположенного на панели корпуса прибора. Здесь же расположена контрольная индикаторная лампа Л нагревателя Н. Штепсельная вилка включается в электрическую сеть с напряжением 220 В.
Изменение длины образца при нагревании по сравнению с его начальной длиной при комнатной температуре фиксируется с помощью индикатора часового типа И. Индикатор часового типа крепится на кронштейне и может поворачиваться вокруг своей оси на 900.
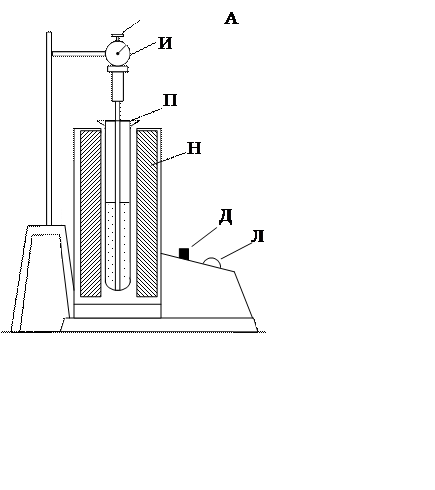 |
Рис. 15.1
Подготовка и проведение измерений
1. Пробирку на ½ объема наполнить водой комнатной температуры.
2. Термометром измерить начальную температуру воды в пробирке t1
3. С помощью штангенциркуля определить начальную длину образца l1
4. Опустить в пробирку образец так, чтобы сферический конец образца упирался в дно коробки.
5. Индикатор И отвести на четверть оборота в сторону до упора.
6. Пробирку с образцом поместить в прибор так, как показано на рис.15.1.
7. Плавно оттянуть шток А индикатора И вверх, установить индикатор над пробиркой и опустить шток в углубление на торце образца С. при работе с индикатором соблюдать осторожность: не допускать резких толчков штока индикатора.
8. Поворотом шкалы Г индикатора И совместить нуль шкалы со стрелкой.
9. Включить питание прибора. При закипании воды в пробирке (через 12-15 минут) по индикатору определить увеличение длины образца Δl . Измерения проводить с точностью до полвины шкалы – 5 микрон. Конечную температуру образца считают равной температуре кипения воды и находят из формулы:
![]()
где Н – атмосферное давление во время проведения опыта.
10. Опыт повторить для каждого образца 305 раз. Перед повторением опыта образец следует остудить, а установку шкалы индикатора производить в течение не более 30-40 секунд, т.к. прибор нагрет, и длительная установка нуля может привести к неточным результатам.
11. Результаты измерений и вычислений занести в табл. 15.1.
12. Произвести математическую обработку результатов.
Для автоматизированной обработки результатов измерений подготовить следующие данные:
1. Число измерений N.
2. Значение начальной температуры t1.
3. Значение конечной температуры t2.
4. Длина тела l1.
5. Приращение длины Δl.
Таблица 15.1
|
№ п/п |
Исследуе- мый материал |
l1, м |
Δl, м |
t1, 0С |
t2, 0С |
α, град-1 |
град-1 |
Δα, град-1 |
α+Δα |
ε= Δα/α |
β, град-1 |
|
1 2 3 с р |
|||||||||||
|
1 2 3 с р |
Контрольные вопросы
1. Что такое тепловое расширение тел?
2. Как объясняется тепловое расширение тел?
3. Что такое абсолютное, относительное удлинение тел?
4. Что называется коэффициентом линейного расширения?
5. Как можно определить нагретого тела?
6. От чего зависит коэффициент линейного расширения α?
7. Как определить объем нагретого тела?
8. Что называется коэффициентом объемного расширения?
9. Каким соотношением связаны между собой коэффициенты линейного и объемного расширения в изотропных и анизотропных веществах?
10. Какие существуют методы измерения температурных коэффициентов?
Литература
1. Матвеев А.Н. Молекулярная физика. – М., 1981. – Гл. V. - §§ 42, 43, 57.
2. Безденежных Е.А., Шевченко А.Ф. Физика. – М., 1978. – Гл 3. - § 31.
3. Попко Ю.М., Князева Л.А. Руководство к практикуму по физике. – М., 1959. – Гл. 4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.